Probability Theory

Definitions

• Experiment

  • A process that generates a set of data .

• Sample Space

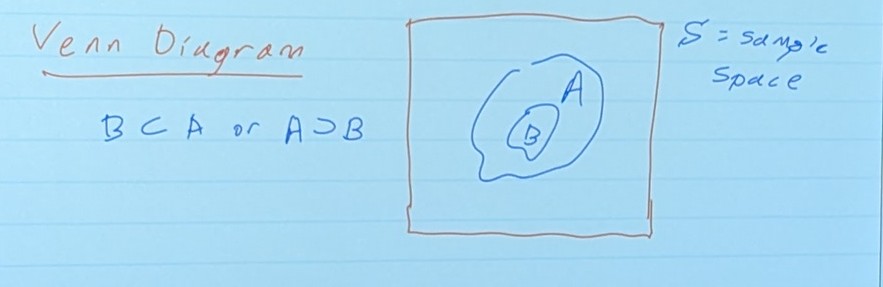
  • The collection of all possible outcomes of the experiment. When we talk about the sample space, we use the capital letter S. These are sometimes hard to characterize. i.e, what are all possible heights that a measured tree could be?

• Event

  • A certain outcome or collection of outcomes have occurred. This is a set. We denote events with capital letters. i.e, A,B etc

• Subsets

  • We say that the event of B is a subset of event A, if B is contained in A

• Venn Diagram

• Null Set: Φ

  • The impossible event (zero area on the Venn Diagram)
  • We can’t have A and B cross

  

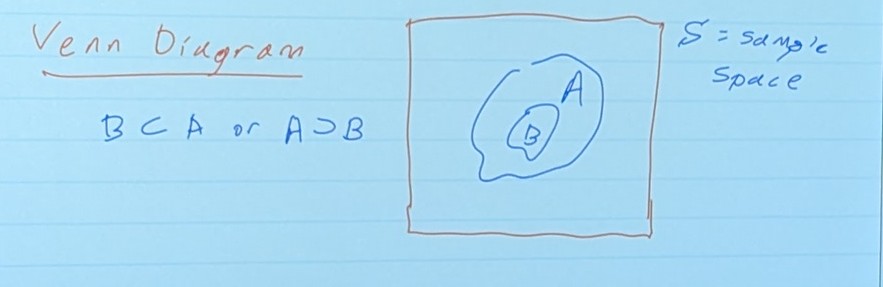
  • In this example, the intersection of A and B is the null set, Φ

• Disjoint

  • If two things can occur, but do not overlap. They are mutually exclusive

Set Operators

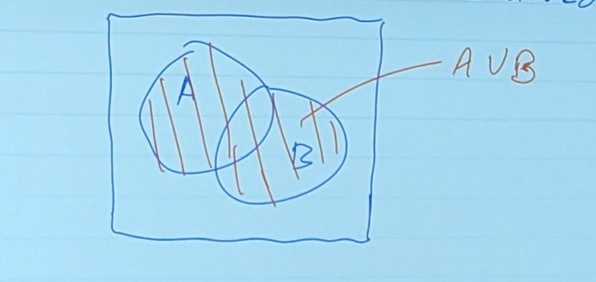
• Union: ∪

  • Basically means A, or B, or both occurred. If A and B are any two sets then A ∪ B (∪)

  

• Intersection: ∩

  • The Intersection of A and B is A ∩ B

  

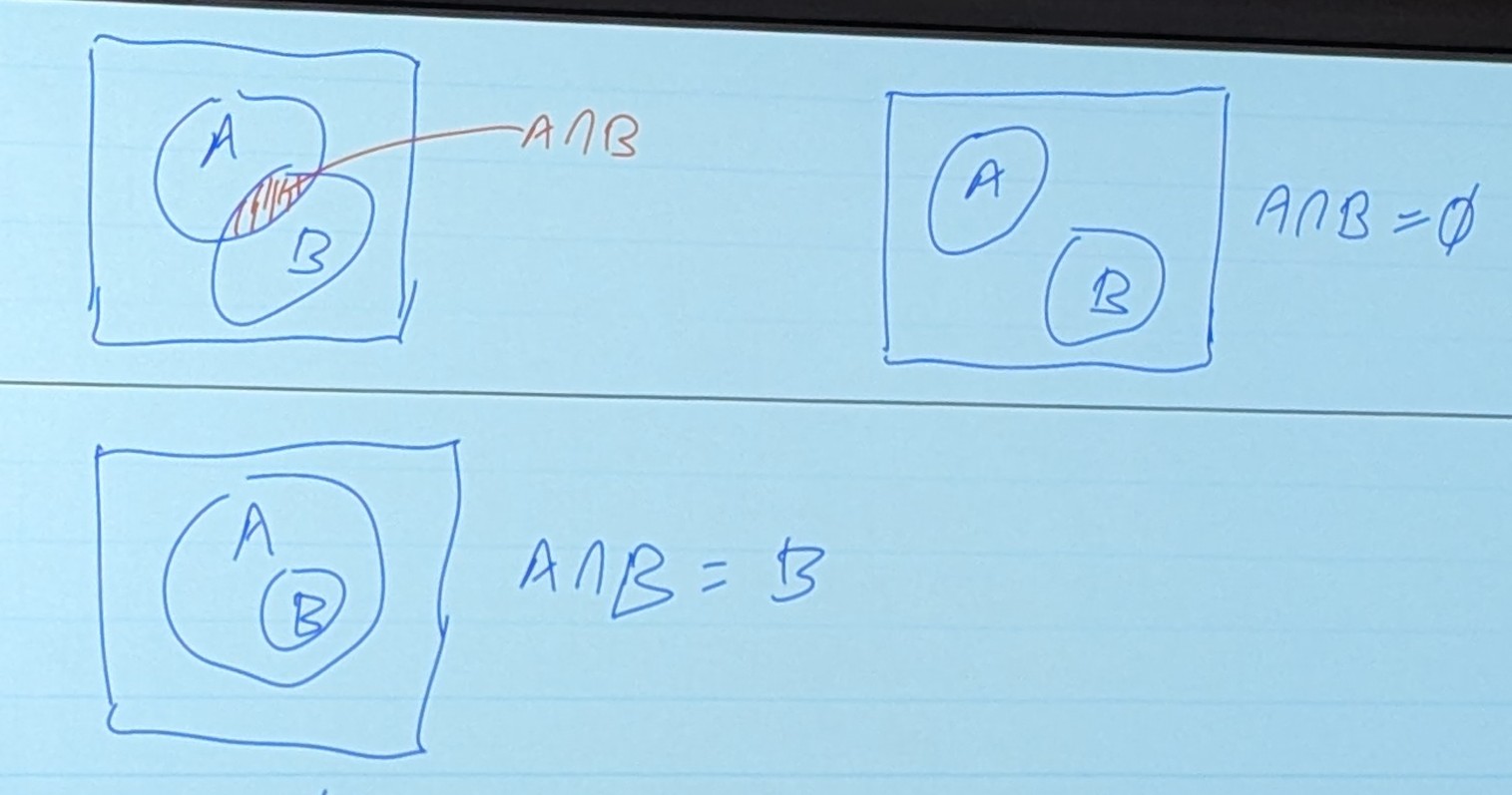
  • In this case, where B is a subset of A, B just is the intersection of A and B

• Compliment: A^c

  • The Compliment of A, is everything outside of A. This is denoted by A^c (the superscript c)

• DeMorgan’s Rules

1. (A ∪ B)^c = A^c ∩ B^c

   

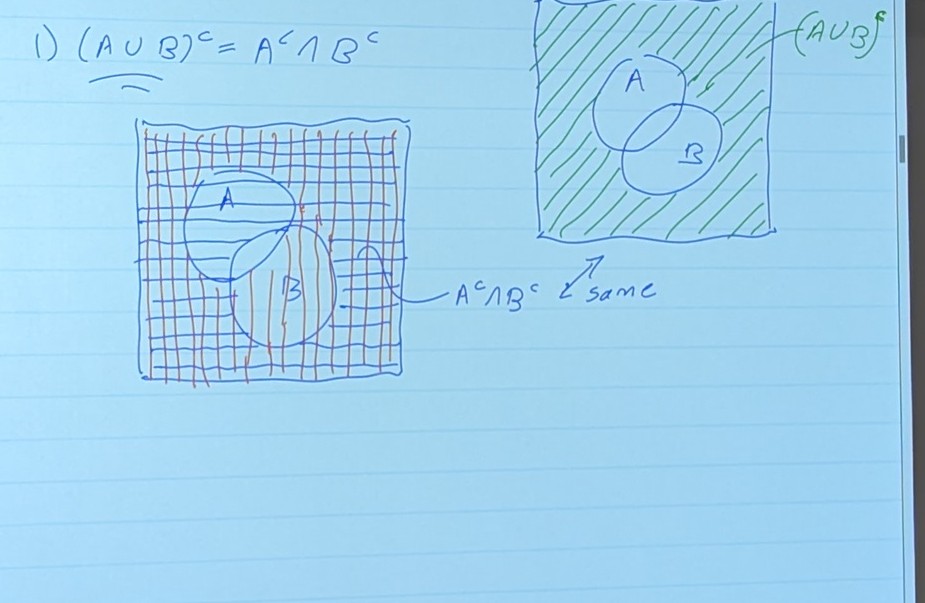
   • These two things, while expressed differently, are the same thing!

2. (A ∩ B)^c = A^c

• Collectively Exhaustive Events

  • A set of events that span the Sample Space. (It has to fill the whole space, no space un-included)

  

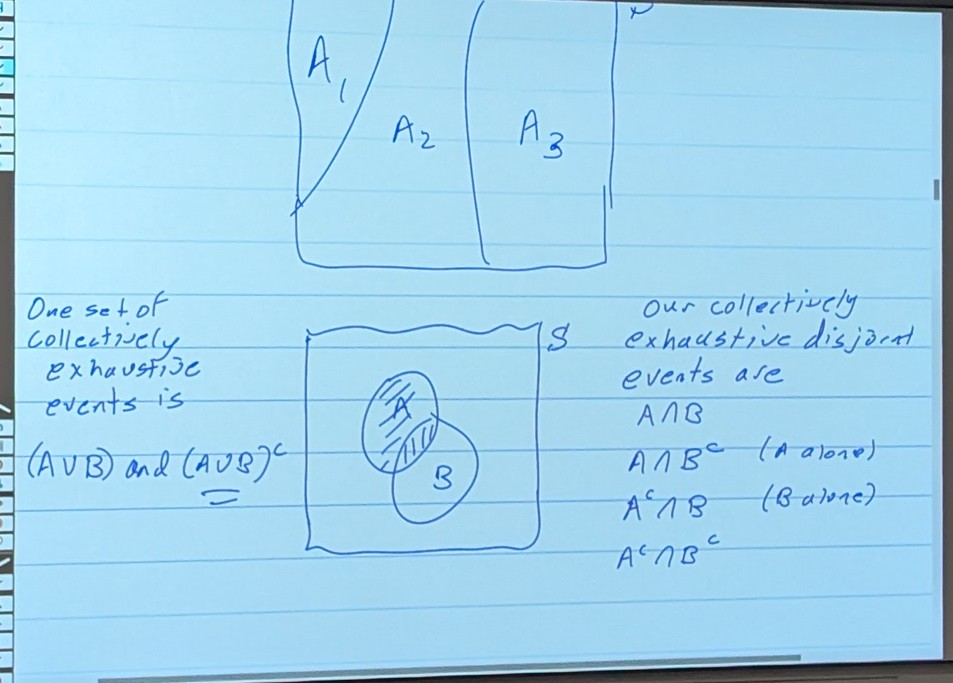
• The first example just fills the whole space. The Second one, uses a bunch of logic to say the same thing.

---

Basic Probability Concepts

“Probability”” is still not clearly defined.

• Interpretation:
  1. Equilikely interpretation ⇾ Was used in early development of probability theory, and was used in games of chance.
  2. Subjective interpretation⇾ Orange juice gold example. Have you ever gotten a orange juice bottle filled with liquid gold? You’d probably think the probability is zero due to past experience. However, it could happen.
  3. Frequency interpretation
  $$P[A]\approx \frac{\text{number of times A occurs}}{\text{number of trials}}$$ We will be concerned with:
  1. Determining probability of events
  2. Updating probabilities given additional information (This is known as Bayes’ Theorem)

The formulation of a probability problem involves 1) Identifying all possible outcomes ⇾ S 2) Assign probabilities to each possible outcome 3) Determine the probability of events

---

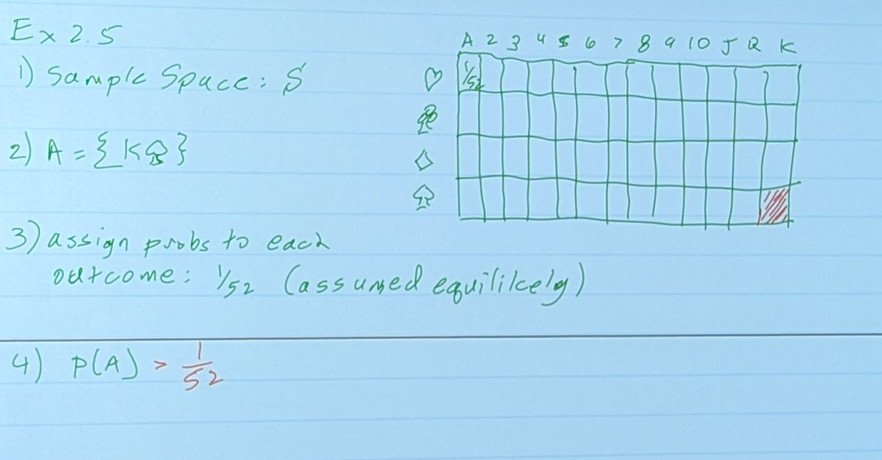
Venn Diagrams are very useful.

---