Distance and Arc Length Calculation

r(t) = Position at a time.

To calculate distance, multiply Speed and Time
Speed is the magnitude of velocity
Distance (S), also known as arclength is equal to the integral of the magnitude of V, times dt (a tiny chunk at that time) from time 1, to time 2.

\int_{t}^{t + Δ t} ∣∣ v ∣∣ d t

This is a new coordinate system
Made up of Unit Tangent (T), Unit Normal (N), and a perpendicular vector known as the Binormal (B)
The Binormal is found by taking the cross product of T and N

B = T \times N

Right hand rule applies here!
- Fingers along T
- Curl fingers towards N.
- Thumb points in direction of B
Another nice trick, is that N always points to the center of curvature.
- If T is going in a direction where the curve is increasing, N is facing up
- If T is going in a direction where the curve is decreasing, N is going down
Another unique thing about this coordinate system, is that T, N and B are all functions of time
T(t), N(t), B(t)
This coordinate system can warp with time

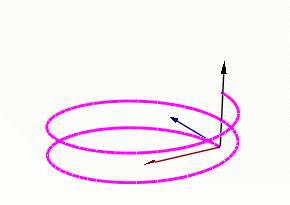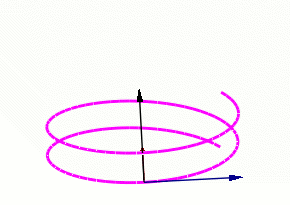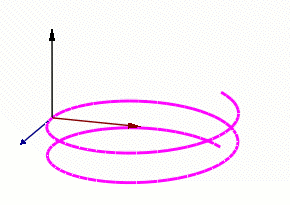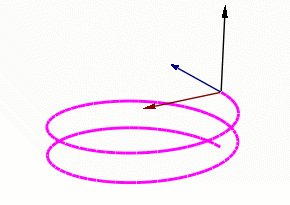
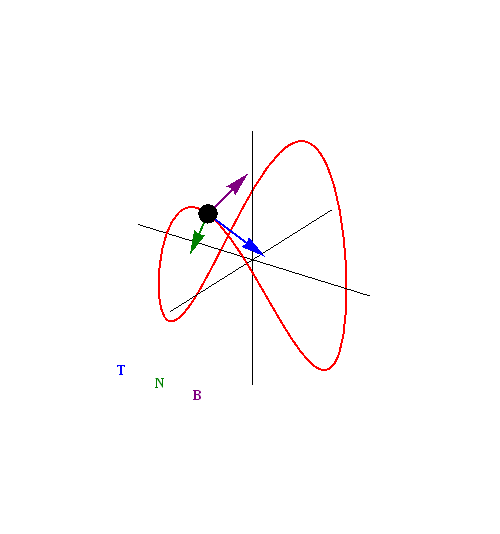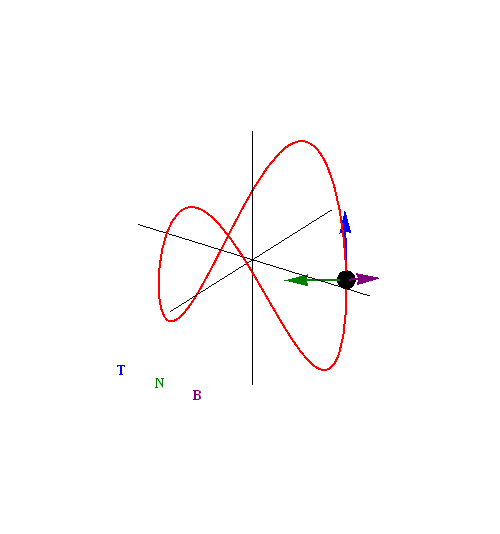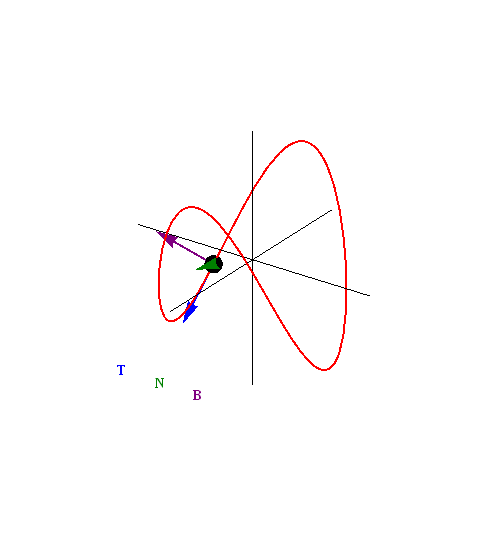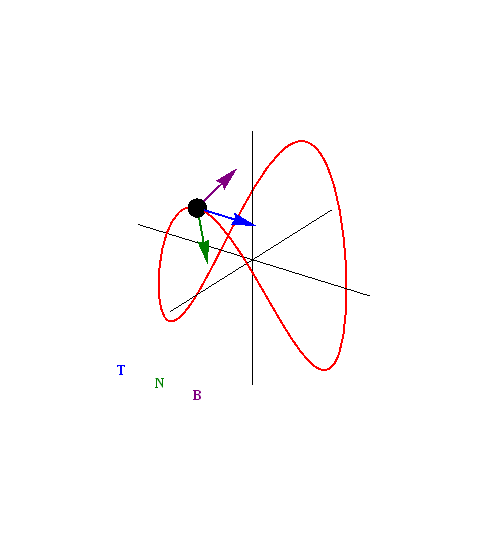
Black = B Blue = T Red = N

What’s cool about Acceleration along a curved path like such, is acceleration has two components

at = Transintestinal Acceleration an = Normal Acceleration

Acceleration

a = a_{t} + a_{n}

at = Transintestinal Acceleration

a_{t} = a \cdot \hat{T}

a_{t} = a \cdot \frac{v}{∣∣ v ∣∣}

an = Normal Acceleration

a_{n} = a \cdot \hat{N}

a_{n} = \frac{∣∣ a \times v ∣∣}{∣∣ v ∣∣}

v = ∣∣ v ∣∣ \hat{T}

V = Magnitude of Velocity (Speed) T = Direction of Unit Tangent (Direction)

\hat{B} = \frac{v \times a}{∣∣ v \times a ∣∣}

This is quite a rigorous proof
Note, in the bottom, he does switch a X v to v X a
- Normally, this would switch the direction of the perpendicular product, but since we’re taking the magnitude, we do not care.

\hat{N} = \hat{B} \times \hat{T}

🌱 Réseau DesAu