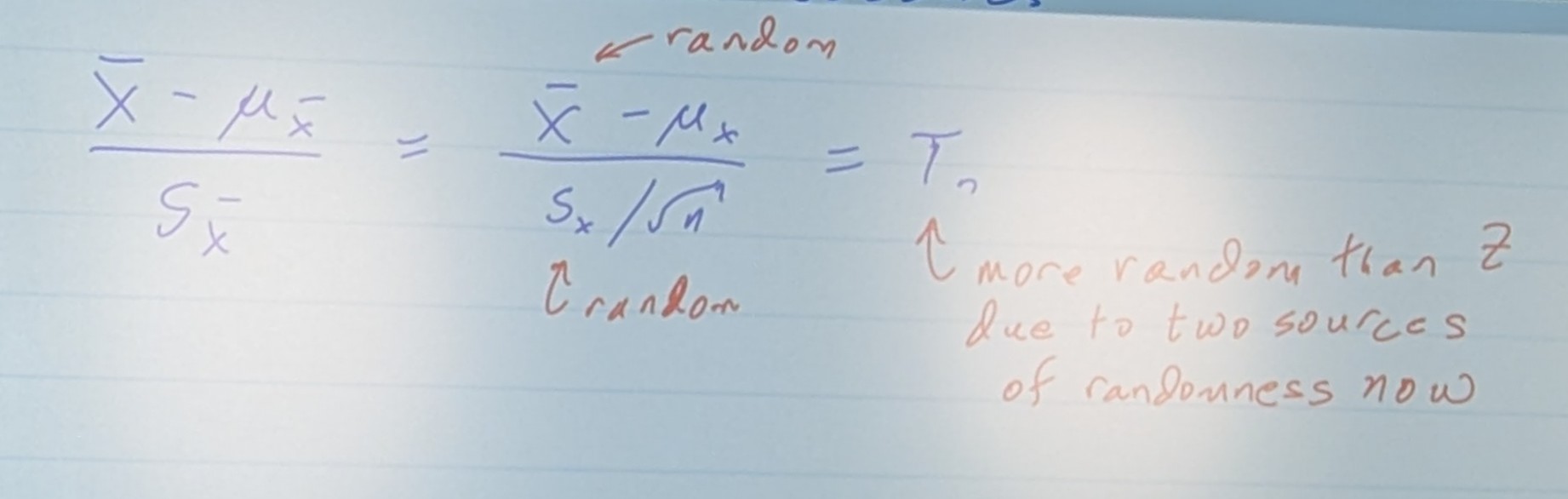Sampling Distributions

Chapter 5: Sampling Distribution

Definition Sheet:

• Population

  • Collection of all possible outcomes of our experiment

• Sample

  • Collection of observations from the population
  • X₁, X₂, … X_n

• Random Sample

  • A set of independent observations

• Statistic

  • A function of one or more random variables

Statistics will be concerned with

• Sample Mean

$$\overline{X}=\frac{1}{n}\sum _{i-1}^n{X}_i$$

• Sample Variance

$$S^2=\frac{1}{n-1}\sum (X_i-\overline{X})$$

Sample mean and Sample Variance are random before we take our observations…

After we’ve taken our random sample, we know X₁, X₂, … X_n, and we get

$$\overline{X}=\frac{1}{n}\sum _{i-1}^n{X}_i$$

Which is a realization of x̄

and

$$S^2=\frac{1}{n-1}\sum (X_i-\overline{X})$$

Which is a realization of S²

One other little note...

X_i has a sample mean as well, but would be quite a bit harder to find. If you were calculating height of a series of students for example, the sample mean of the group of students would be x̄ for example.

However, this isn’t representative of EVERY student on the planet, or the ENTIRE Population. You would need to find the sample mean (μ) of X_i for that.

If I repeat the process, and observe another set of observations, I’ll get a new X₁, X₂, … X_n, and a new x̄ and S²

---

Example One

μ_x = E(x_i) 100Ω σ = 10Ω N = 25 We know this is a Random Distribution (follows a normal distribution) Let X_i = X of I resistor

P(\overline{X}<95) = P(Z_1 < \frac{95 -\mu_\overline{X}}{\sigma_\overline{X}} = P(Z < \frac{95 -\mu_{X}}{\frac{\sigma_x}{\sqrt{n}}}) =1-\Phi(2.5) = 1 - 0.99379 =\underline{0.00621}

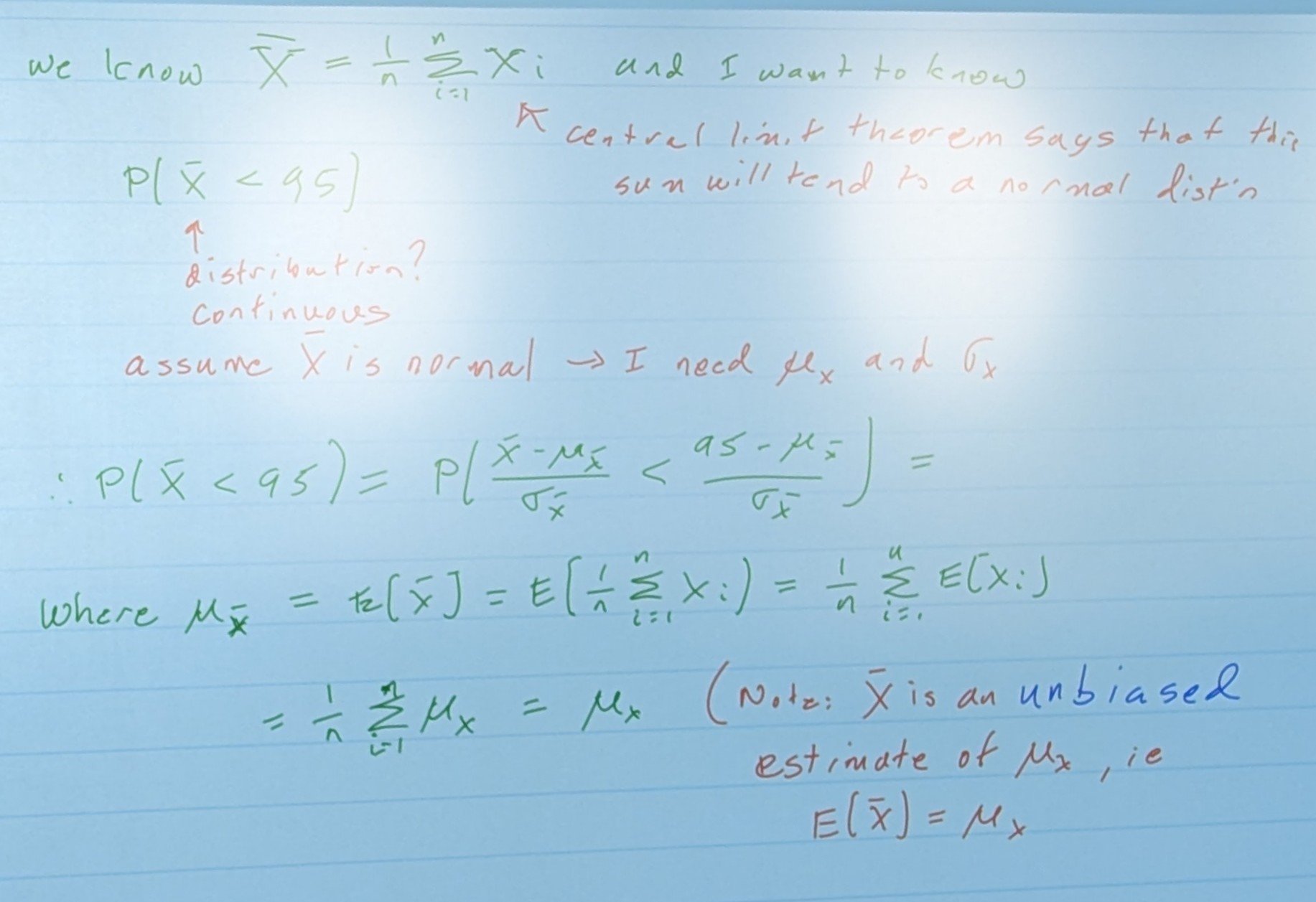
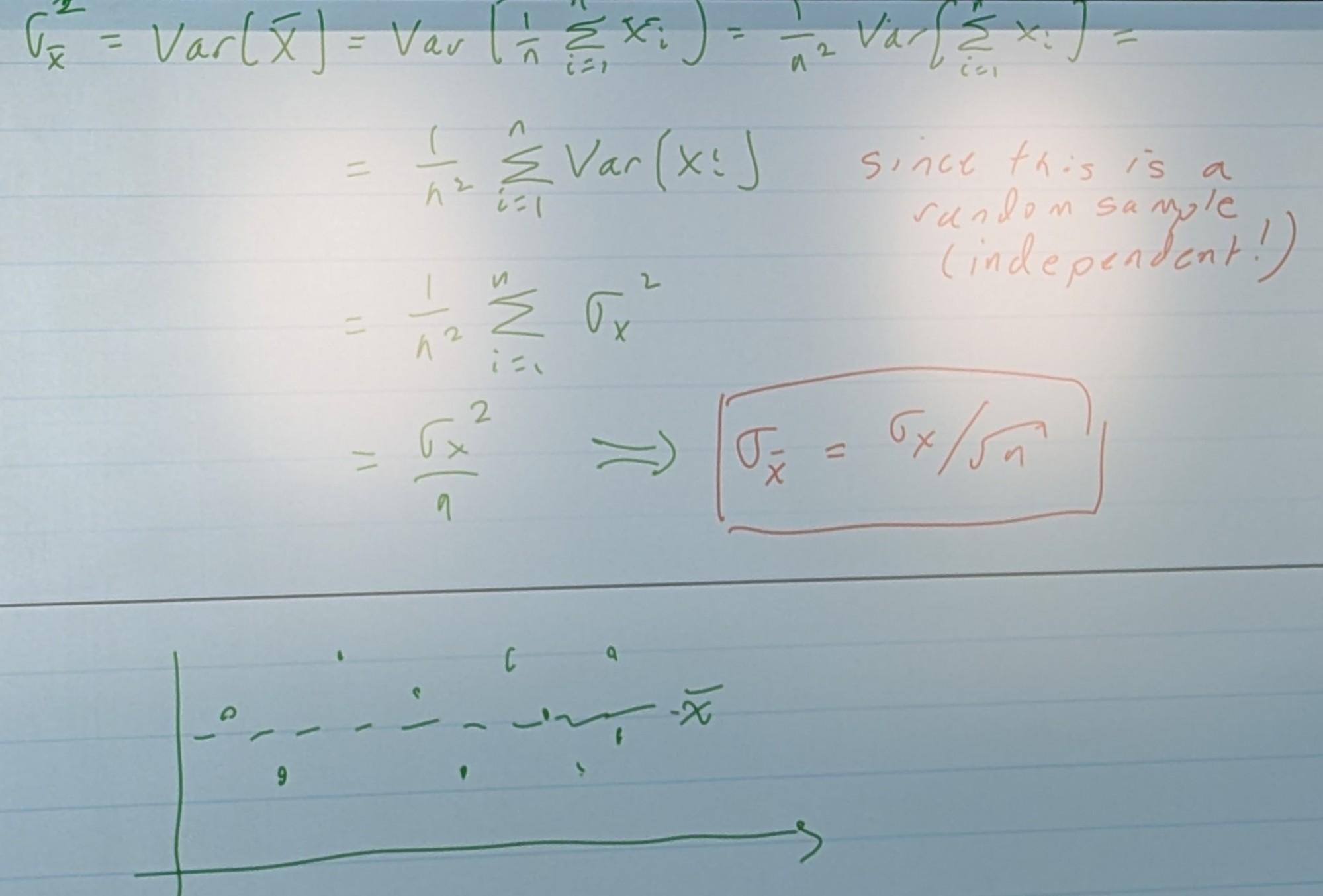
Remember, Φ is pulled from a lookup table.

---

Example Two

μ_x = E(x_i) 1.01 σ = 0.003 N = 9 (Here, we have to assume “Random Samples”. Otherwise, this isn’t doable.) We know this is a Random Distribution (follows a normal distribution)

We want to find:

P((x̄ < 1.009) U (x̄ > 1.011))

Distribution? We need; μ_x̄ and σ_x̄

μ_x̄ = μ_x, σ_x̄ = $\frac{{\sigma }_x}{\sqrt{n}}$

Here, we’ll find the probability for one half of the curve, and then double it (because they are the same thing on each side)

---

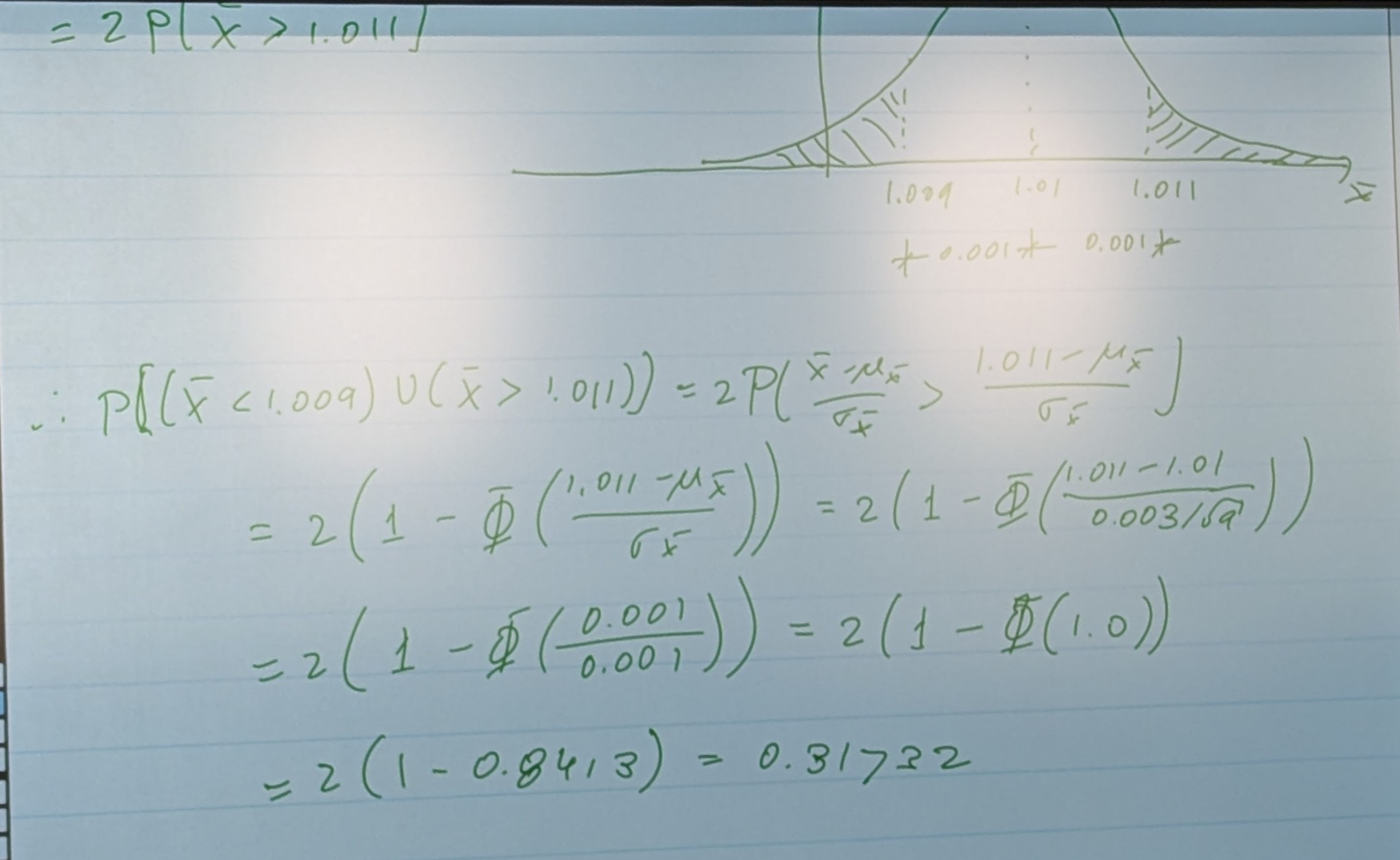
Now, what happens if I don’t know σ_x?

We must now estimate σ_x with S_x

where S_x² =

$$S_x^2=\frac{1}{n-1}\sum (X_i-\overline{X}{)}^2$$

So, our standardization now becomes: