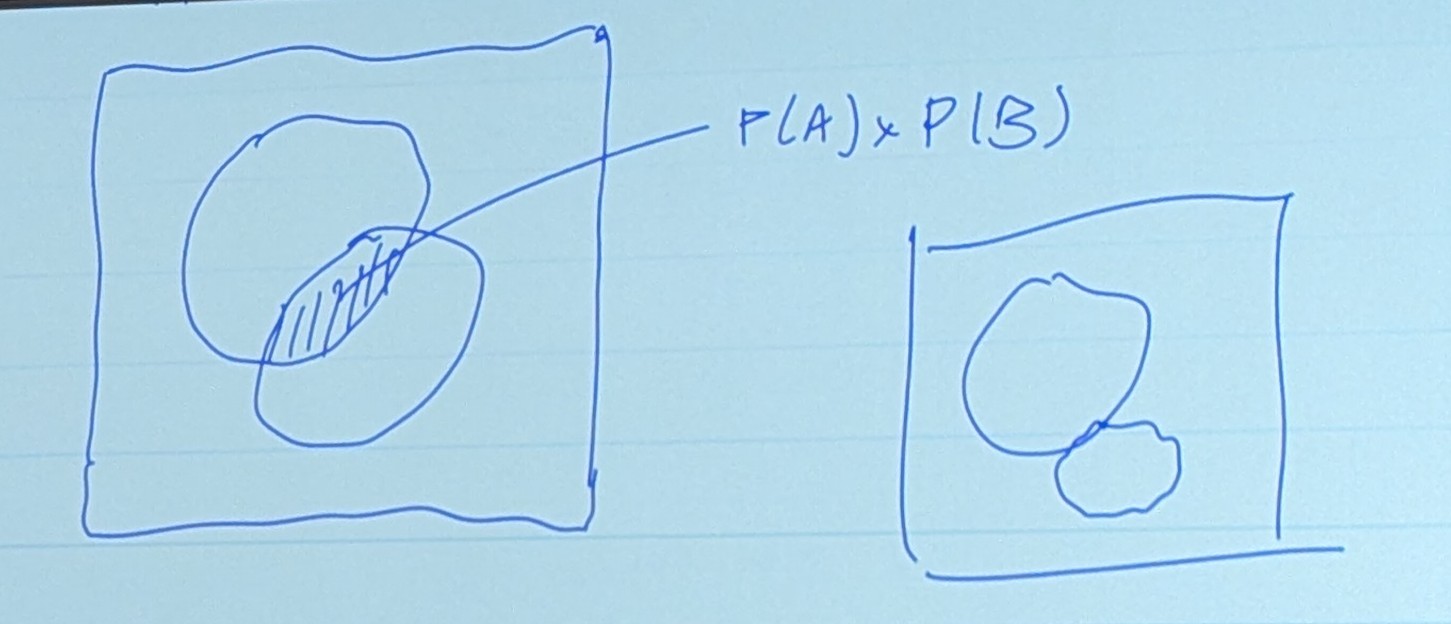
Independence vs Disjunction

Independence

If events A and B are independent, then the occurrence of one does not effect the probability of occurrence of the other.

I.e

$$P(A|B)=P(A)$$

If A and B are independent.

Just because B happened, doesn’t make A any more likely.

This means that

$$P(A\cap B)=P(A)P(B)$$

P(A)P(B) (the product of the two probabilities) is much simpler to calculate!

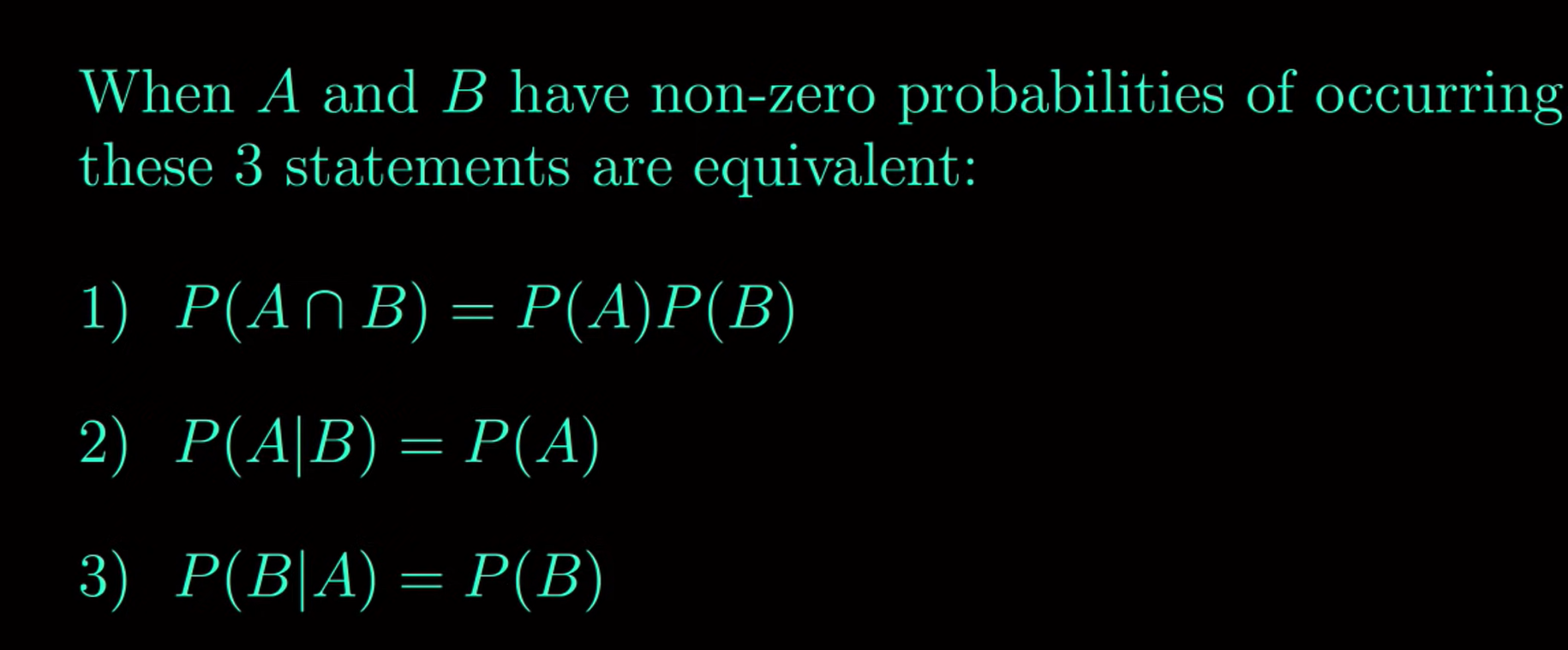
• If these are true, A and B are independent
• If these are false, A and B are dependent

Note

“independent and “disjoint” are opposites

If A and B are disjoint then $P(A\cap B)=0\ne P(A)$

If Independent, A and B must overlap by a specific amount

Any time you see a probability of an intersection, you should ask “are those independent?”

Consider $P(A\cap B\cap C)=P(A|B\cap C)P(B|C)P(C)$

$$=P(A)P(B)P(C)\text{if independent}$$

So the rules!

P(Union) ← Are they disjoint?

P(Intersection) ← Are they independent?

---

Example 1

Here, the machines being independent saves us a lot of time!

---