Multivariable Integration

Definite Integral in Multivariable Calculus

• Currently, we know the definite integral as the area under the curve of a function g(x) between two points A, and B
  • g(x) being the height
  • dx being the width

Now, we can extend this to functions of several variables:

---

Indefinite Integrals: Partial integration

Partial integration with respect to x

$$\int \frac{df(x,y)}{dx}dx=f(x,y)+c(y)$$

Partial integration with respect to y

$$\int \frac{df(x,y)}{dy}dy=f(x,y)+c(x)$$

The previously known “+c” integration constant, now acts more as a function created by the integration, depending on what we are taking the integral with respect to.

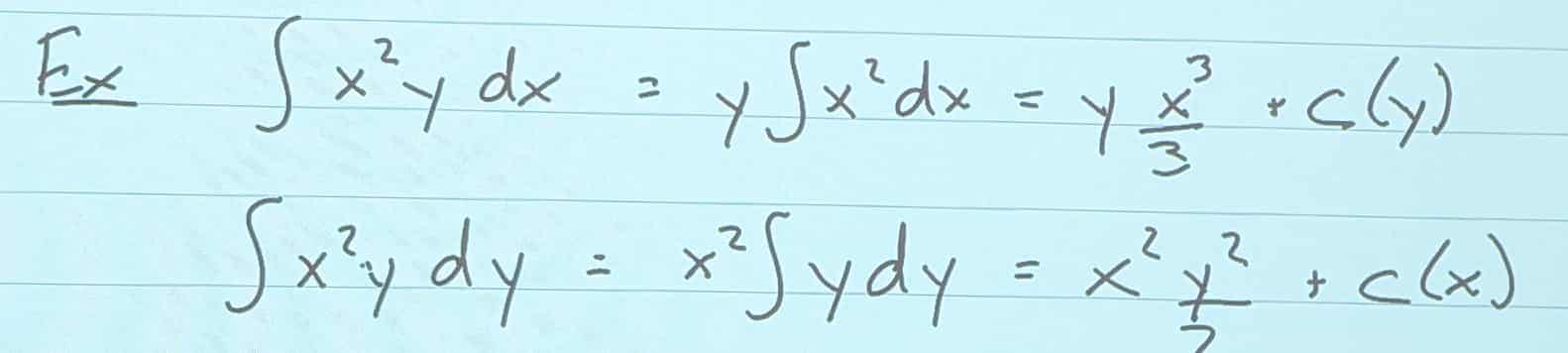
• Partial derivatives allowed us to find the gradient given a function.

• Partial Integration allows us to compute the function given its gradients.

• We can also do this in 3D!

---

”Definite” Integrals: Partial integration

(Partial Integration with limits)

$${\int }_{x=a}^b\frac{df}{dx}dx=f(x,y+c(y)){|}_{x=a}^b$$

Plug in A and B to be…

$$(f(b,y)+c(y))-(f(a,y)+c(y))$$ $$f(b,y)-f(a,y)$$

Now, this is just a function of Y (no X)

Now, what would happen if limits for X involved Y? You would still end up with a function of only Y

Double Integrals

• Definite multivariable integrals in 2D
• Volume under the surface g(x,y) above region R_xy

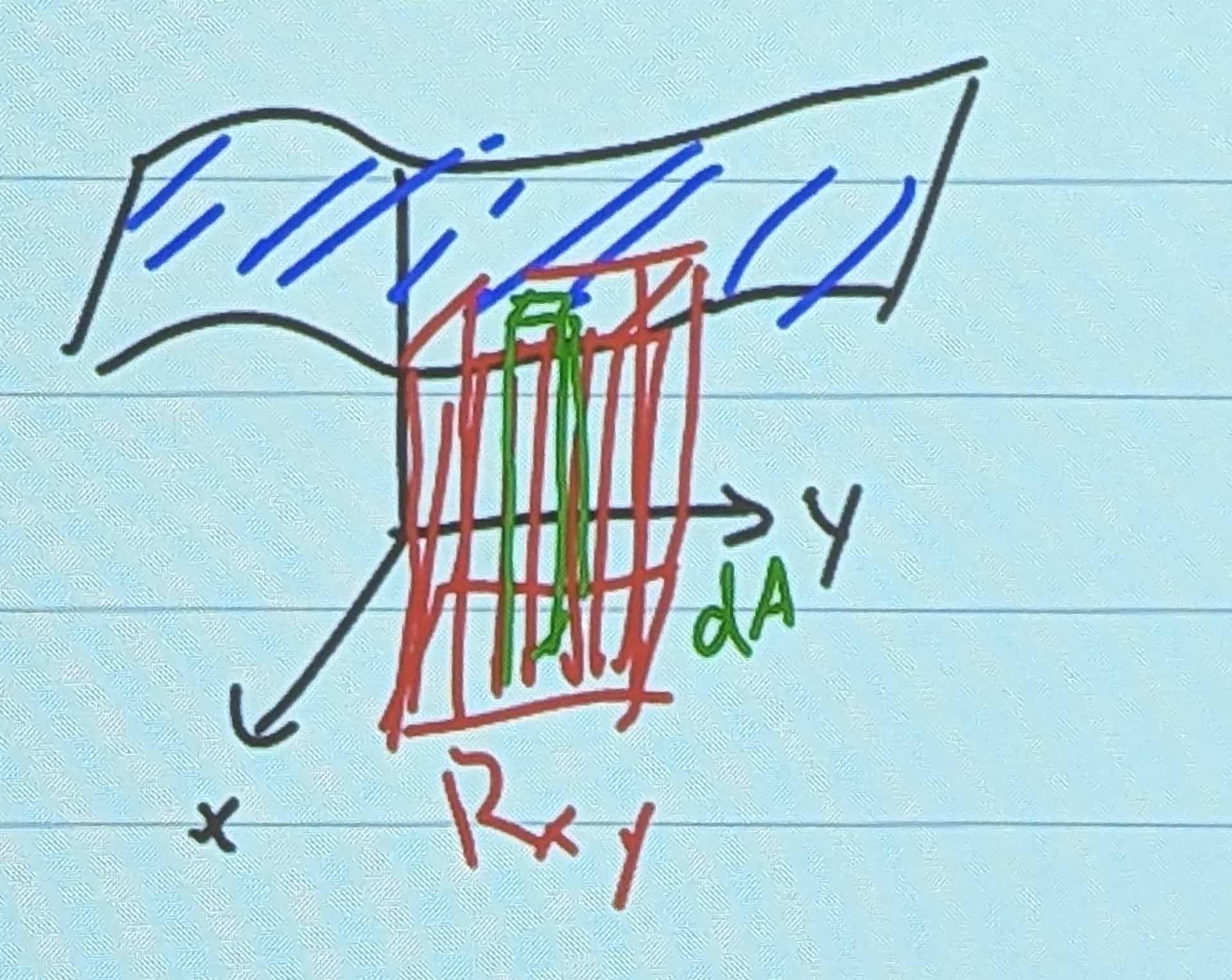
(dA is a small chunk)

$$\iint g(x,y)dA=\text{Volume}$$

How do we do a double integral?

• Math is no harder than 1D
• 2D is just has an extra step

The Tricky part is not integrating, but rather defining R (setting limits)

Double Integrals on Rectangles

In rectangles, one integral deals with X, and the other deals with Y

One thing to note, is that the order does not matter!

• In this example, X is done first, and then Y. However, you could also do Y first, then X
• However, it is important to write your dx’s and dy’s in the order that you are integrating them. It is still correct, however, can trip you up later on.

Double Integrals on General Regions

Type One (Top and Bottom are functions/Curly)

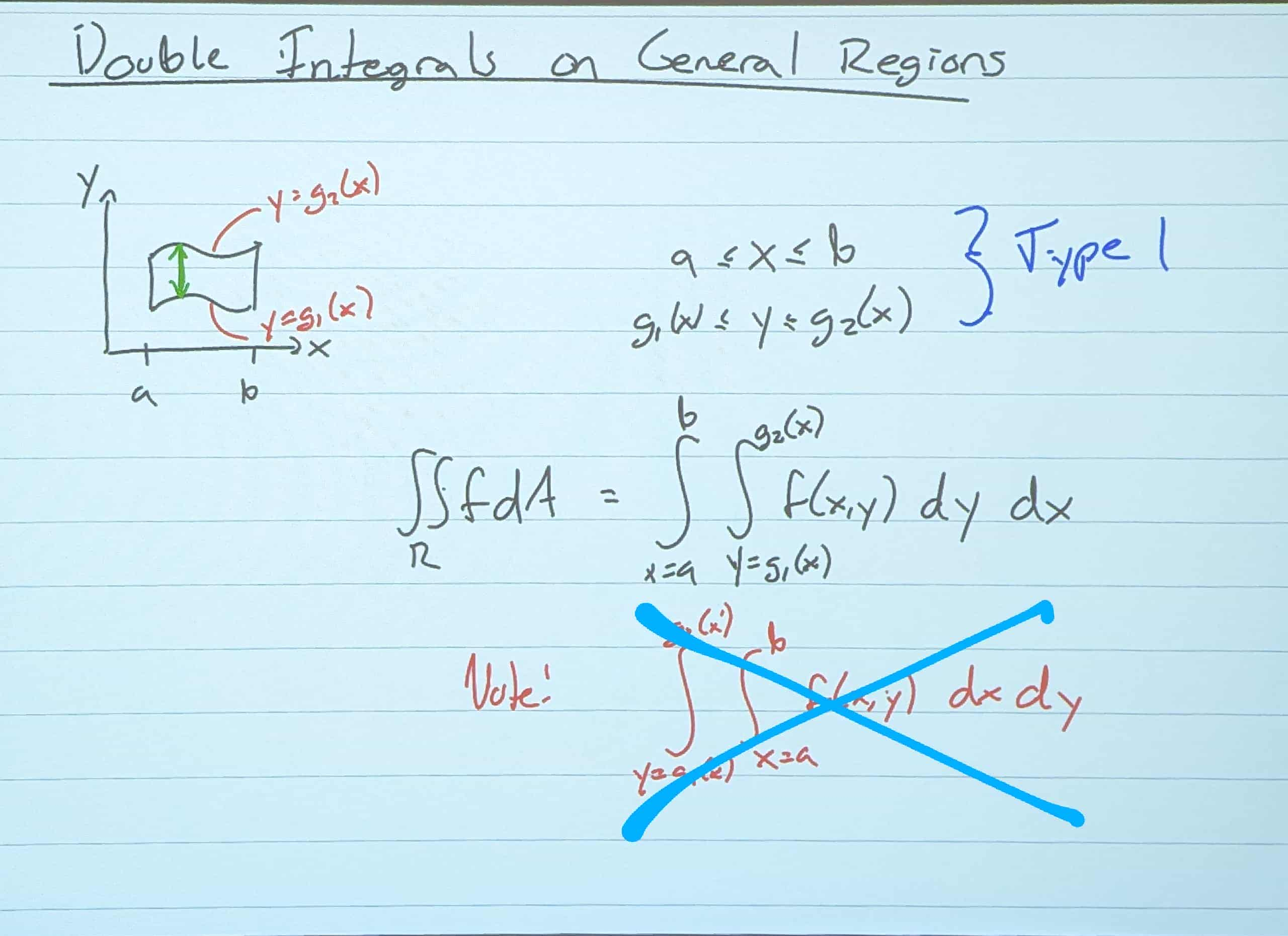
• Here, instead of setting proper bounds like a square, we are integrating in between two functions.
• When you integrate this kind of function, where you are integrating in between level of Y, you MUST integrate Y before X

Type Two (Sides are functions/Curly)

• Same idea here! You must integrate in terms of X before Y, if you are integrating in between two functions in X.

• An important note for these, is if you are taking an integral in Y, you need to re-arrange the bounds in terms of Y