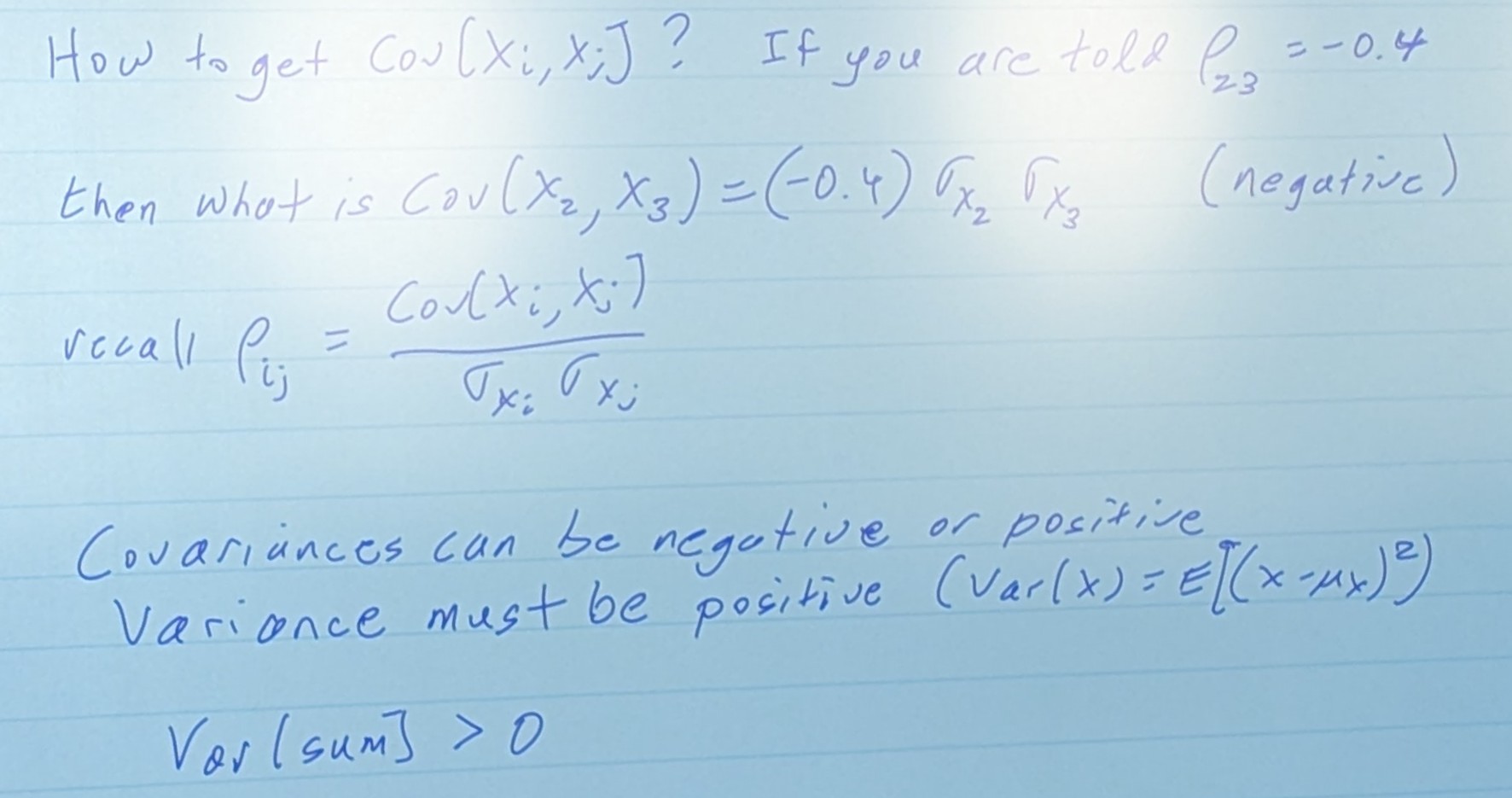Random Variables Continued

Main Descriptors

• Mean: μ
  • Balance point, or the first moment

$${\int }_{\infty }^{\infty }{f}_x(x)dx$$ $$f_x(x)=P(X=x)$$

• Median: x͂
  • Point which divides the distribution in half
  • If the distribution is symmetric about the mean, then x͂ = μ_x

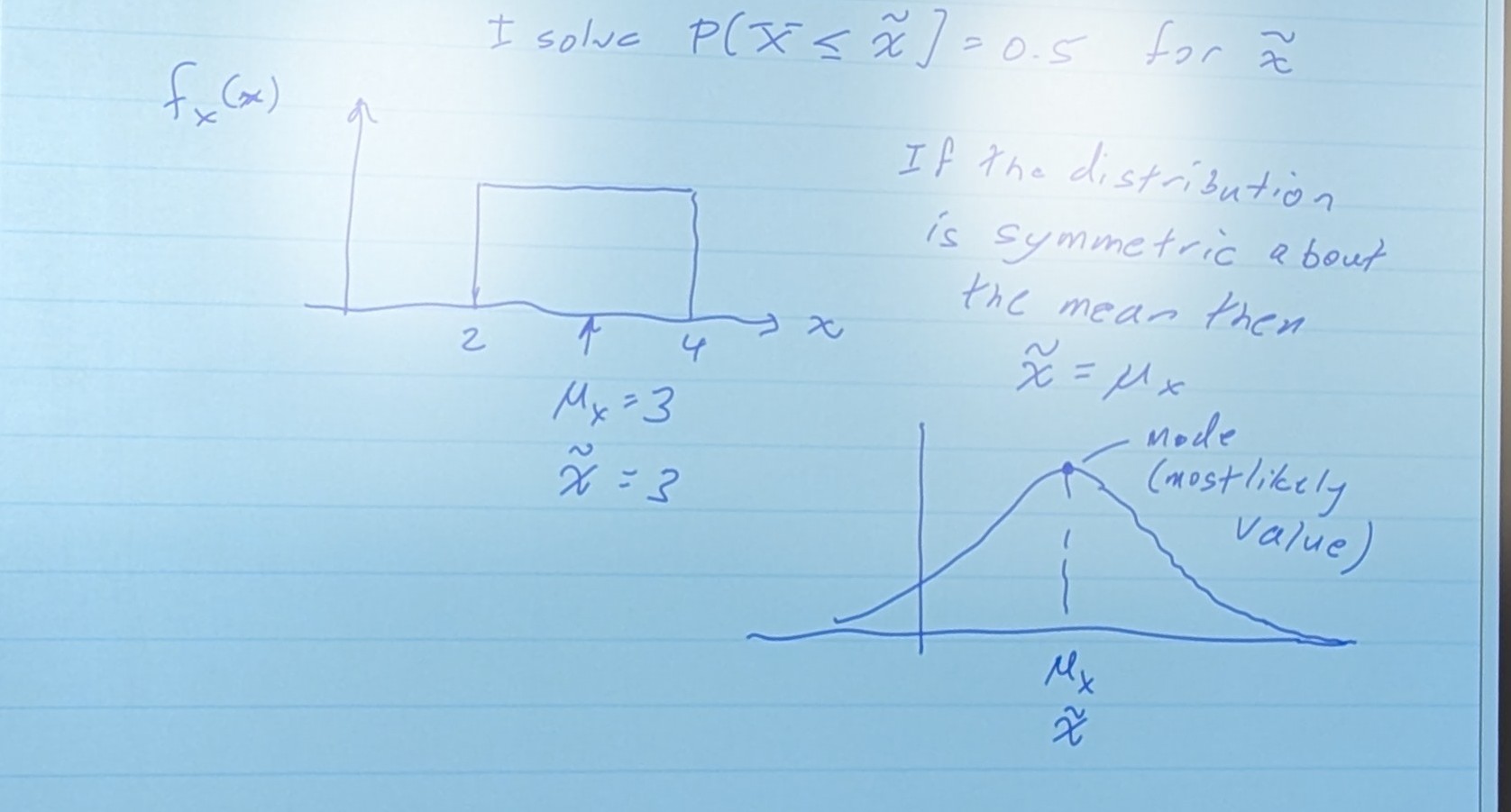
• Mode
  • Most common, or likely point. Usually the highest point on one of these PDF graphs.

---

Expectation Operator

$$E(\text{ANYTHING})=\sum _{\text{all}\text{things}}(anything)\times P(\text{ANYTHING}=\text{anything})$$

When I say anything, I really mean any function of X

• E(X) = Sum of all x’s times their probability of occurrence

• E(sum) = Sum of Expectations

What about the expectation of a constant times X? E(ax)

$${\int }_{\infty }^{\infty }{f}_x(ax)dx$$ $$a{\int }_{\infty }^{\infty }{f}_x(x)dx$$ $$aE(X)$$

What about the expectation of a constant, just normally?

$$E(A)=A$$

• I mean, the number isn’t random anymore. The expectation of two… would just be two you’d hope, right?

*What about the expectation of a constant, plus a constant times X?

$$E(a+bX)=E(a)+E(bX)=a+bE(X)$$

---

Measures of Variability

σ = Standard Deviation σ² = Varience

There is a proof to say:

$$Var(X)=E(x^2)-E^2(X)$$ $$E(X^2)=Var(X)+E^2(X)$$

You can tough it out through that integral, or you can use the formula

Covarience

Now, let’s think about two random variables, X and Y

• Here, there seems to be a linear dependence between X and Y

• Here, there doesn’t seem to be any dependence at all in between X and Y. Just completely random.

• In this case, we have non linear dependence. There’s no linear dependence here! If we draw our line of best fit, there’s a pretty telling sign here that we have no linear dependence.

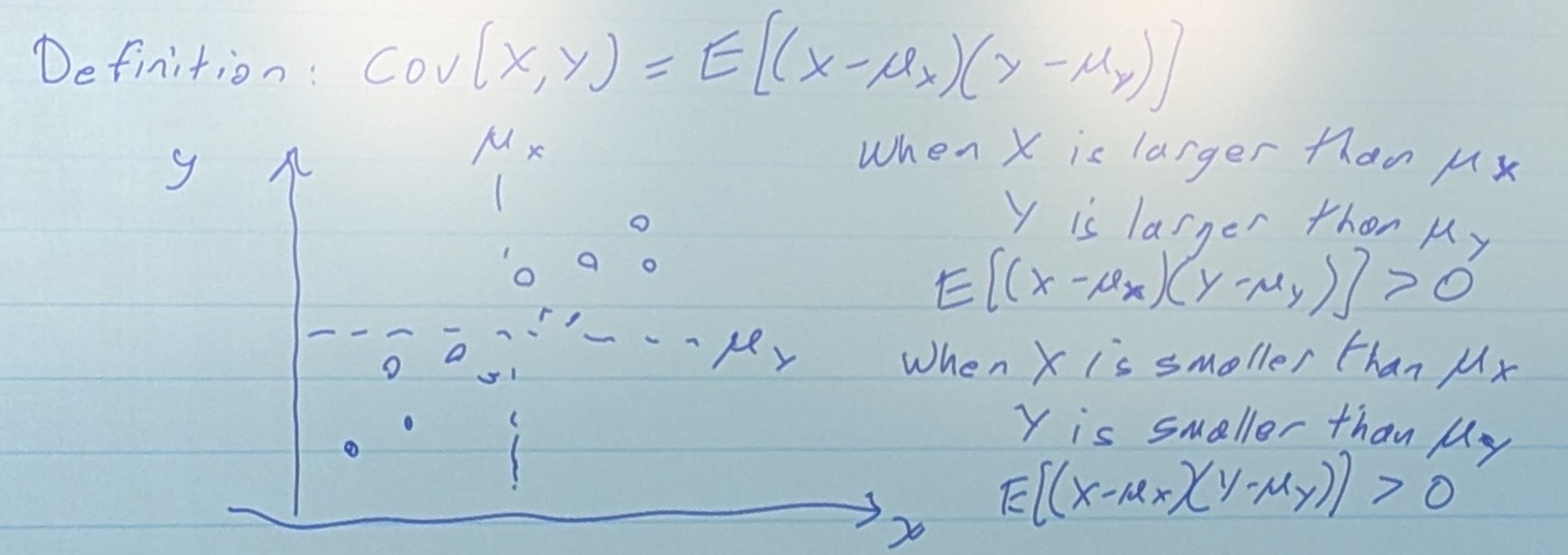
• So, Cov(X,Y) has the same sign as the slope.

There is a proof to say,

$$Cov(x,y)=E(XY)-E(X)E(Y$$ $$E(XY)=Cov(x,y)+E(X)E(Y)$$

The E(XY) term is not trivial to find, and is usually either given, or solved for using the covariance.

Another point, if the Covariance is completely linearly dependent, like Y = X for example,

$$Cov(X,Y)=E(XY)-E(X)E(Y)=E(X^2)-E^{(}X)=\text{Varience}$$

So if the Covariance is completely linearly dependent, it is directly equal to Varience

---

Correlation Coefficient

$$\text{Correlation}\text{Coefficient}={\rho }_{xy}=\frac{\text{Cov}(x,y)}{({\sigma }_X)({\sigma }_Y)}$$

If X and Y are uncorrelated (Cov(XY) = 0), or independent (Cov(X,Y) = 0) and no other dependence

$$Cov(X,Y)=E(XY)-E(X)E(Y)=0$$ $$E(XY)=E(X)E(Y)$$

---

Linear Combinations

(or just a fancy way to say sum)

So typically in engineering, we have a total load capacity made up of smaller loads.

Say Y = X₁ + X₂

If I know about X₁ and X₂, what is the mean and variance of Y?

$$\text{Mean},{\mu }_y=E(Y)=E(X_1+X_2)=E(X_1)+E(X_2)={\mu }_{x1}+{\mu }_{x2}$$

Variance is a little more complicated…

There is a proof to show that….

We get that

$$\text{Var(sum)}=\text{sum}\text{of}\text{all}\text{the}\text{possible}\text{covariances.}$$

For example

$$Var(Y)=Var(X_1+X_2)=Var(X_1)+2Cov(X_1,X_2)+Var(X_2)$$

The general rule is

$$\sum _{i=1}^n\sum _{j=1}^n{a}_i{a}_{j}Cov(X_i,X_j)$$