Total Probability Theorem, and Event Trees

Total Probability Theorem

• Often, we want the total probability of failure of a system, P(F)

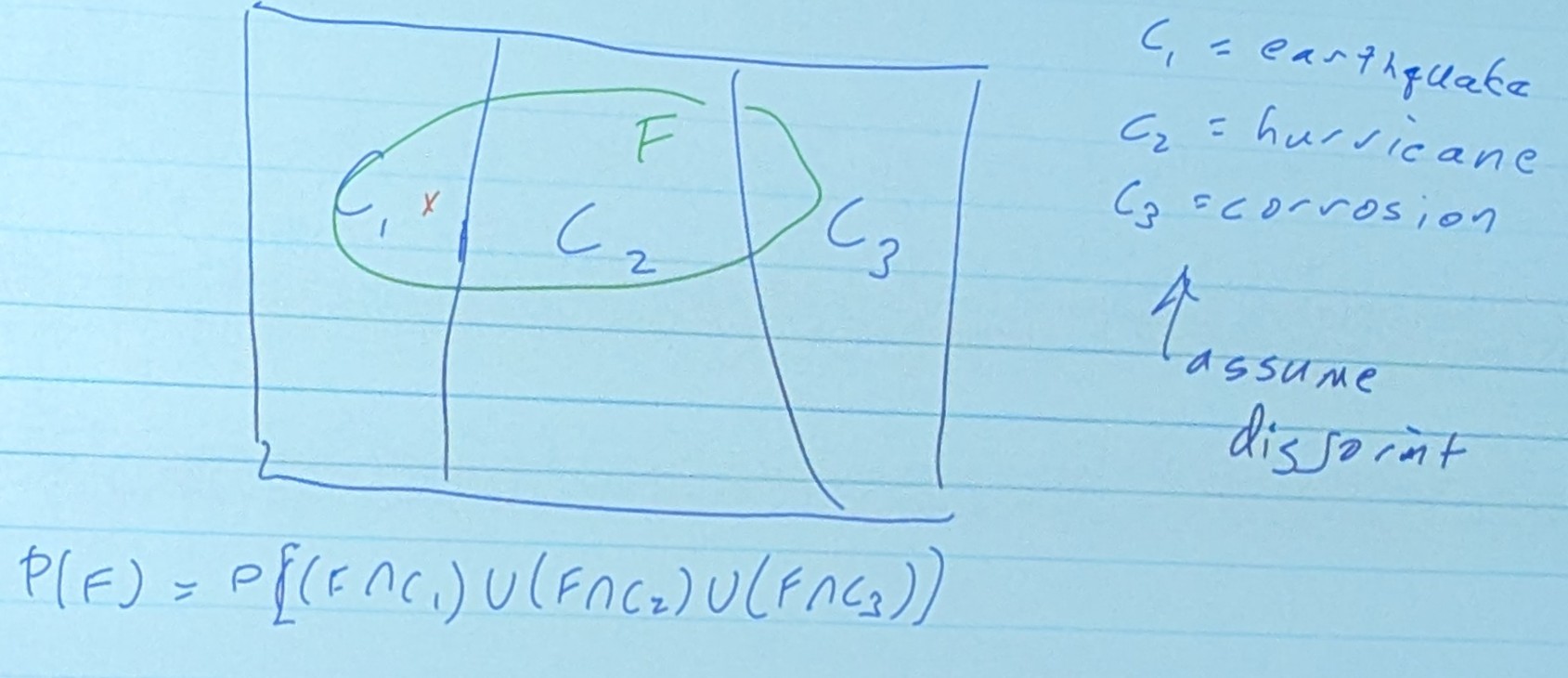
• Since we are assuming unions are disjoint in this case, we can just add the unions

$$P(F\cap C_1)+P(F\cap C_2)+P(F\cap C_3)$$

and for the probability of the whole thing…

$$P(F|C_1)P(C_1)+P(F|C_2)P(C_2)+P(F|C_3)P(C_3$$

P(C₁) = Probability of an earthquake happening P(F|C₁) = Probability of the building failing given an earthquake happens

---

What happens if the events are disjoint?

Consider just two causes:

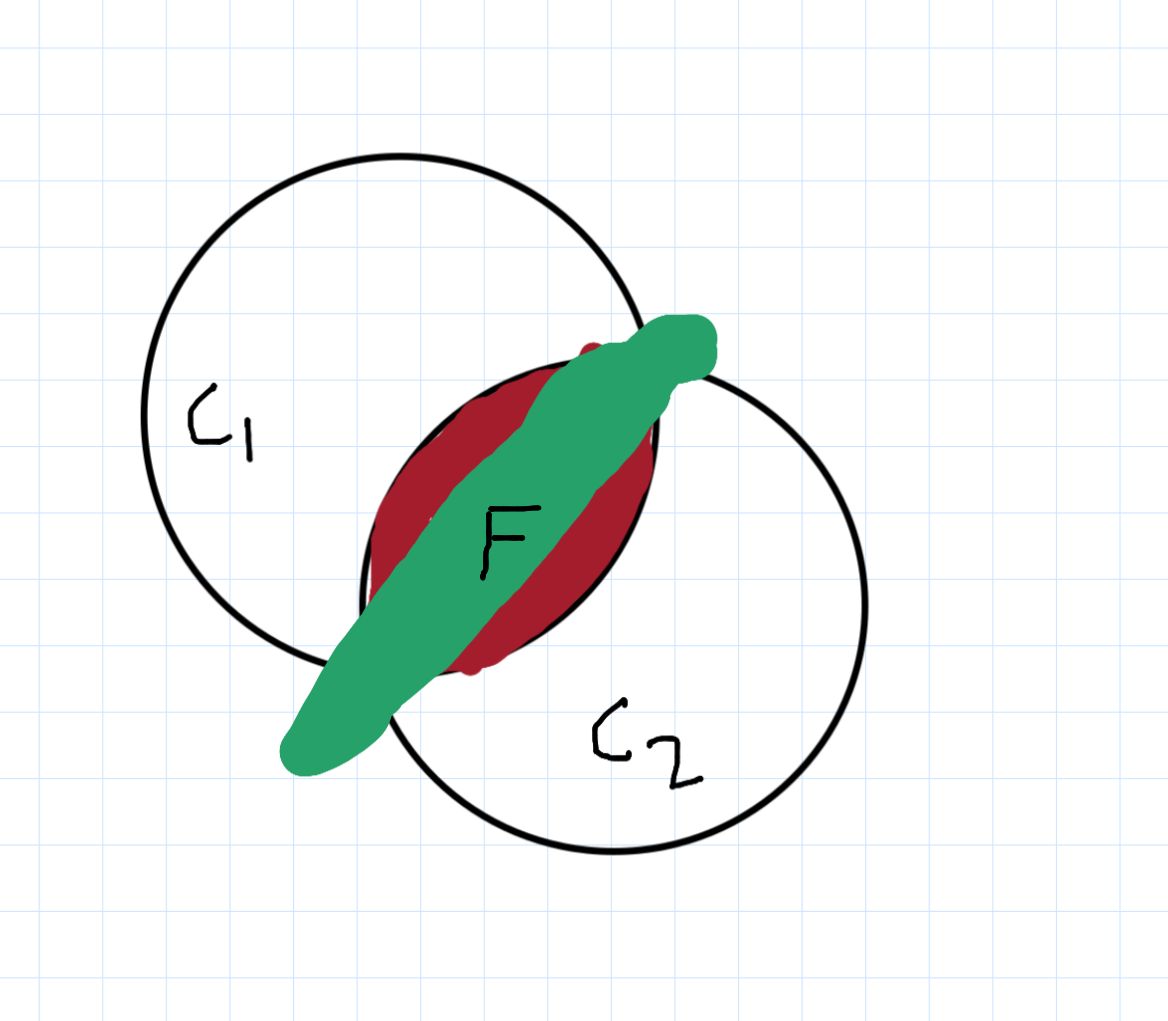
P(F) = Sum of all disjoint areas in the Venn Diagram

Event Trees

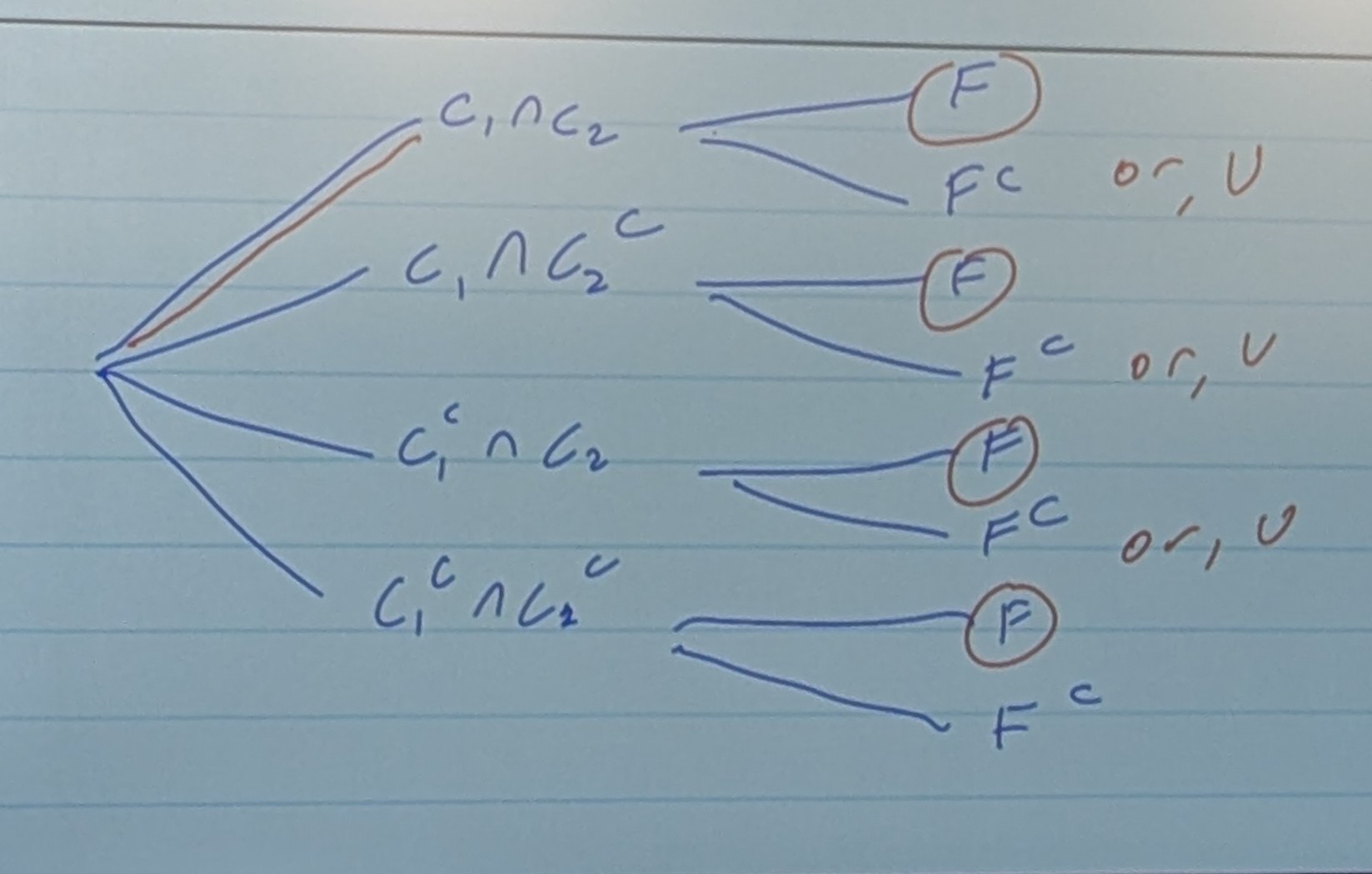
This is another tool for assisting in solving probability:

• We can only be on one branch at a time (disjoint)
• Each node’s probabilities must add up to 1.0 (collectively exhaustive)

---

Example 1

C = Conservatives are elected N = NDP are elected F = Event that facility is funded

Event Tree

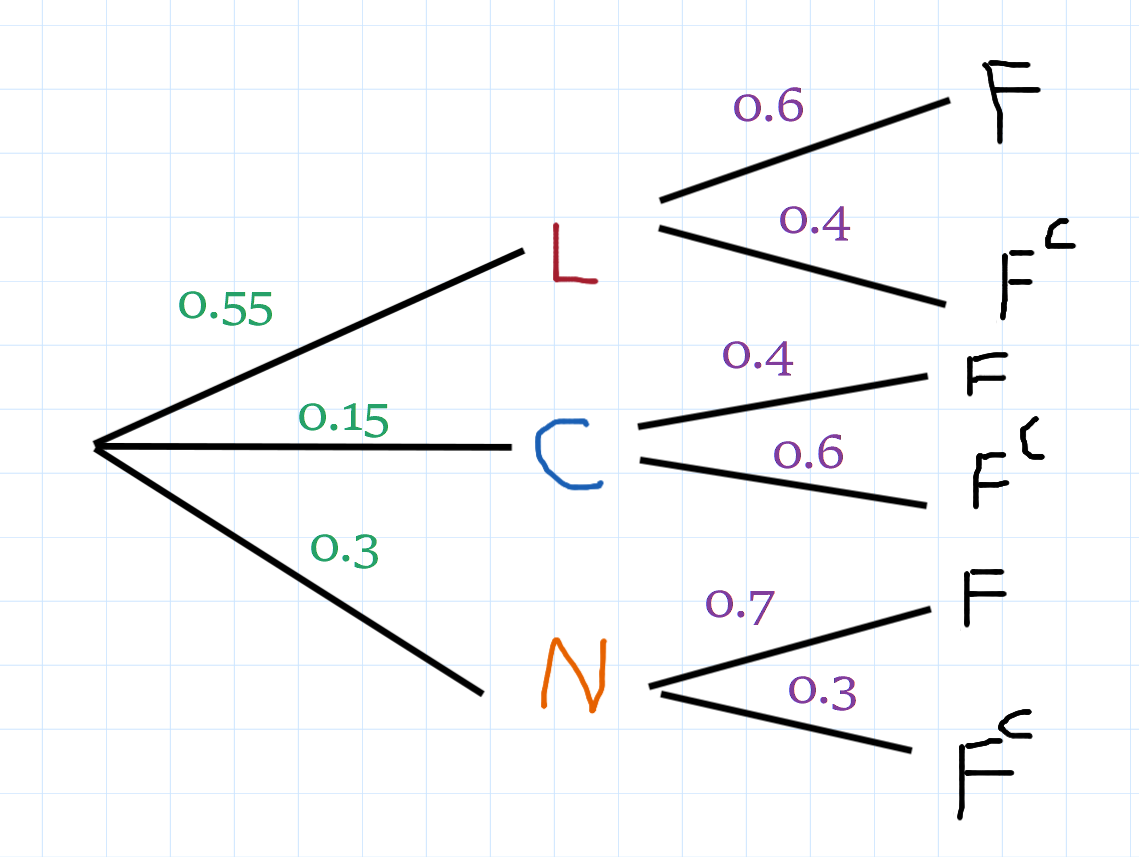
I want to find the percent chance of funding for this project

$$P(F)=0.6(0.55)+0.4(0.15)+0.7(0.3)=\underline{0.6}$$

So we have a 60% chance of receiving funding.

---

Bayes Theorem

$$P(B|A)=\frac{P(A|B)P(B)}{P(A)}$$

Bayes Theorem is great at determining the conditional probability of events.

---

Example 2

In this case, let’s say that we found out that the project got funding. However, say we are on a vacation in Cancun with our nuclear money, and have no idea who funded it. In this case, what are the chances that the Tories funded it?

Here, we can use Bayes’ Theorem

$$P(B|A)=\frac{P(A|B)P(B)}{P(A)}$$ $$P(C|F)=\frac{P(F|C)P(C)}{P(F|L)P(L)+P(F|C)P(C)+P(F|N)P(N)}$$

P(C) = Probability of Tories winning P(F|C) = Probability of Tories funding the project given that they win the election

$$P(C|F)=\frac{(0.4)(0.15)}{0.60}=\underline{0.10}$$

So, there is a 10% chance that the Tories funded the power plant, if we know that it got funded.

---