Best Approximation isn’t all that bad!
- Best approximation uses the projection formula to approximate fits of lines
An example of projecting Y onto U, a vector perpendicular with W.
Here is an easy example of such!
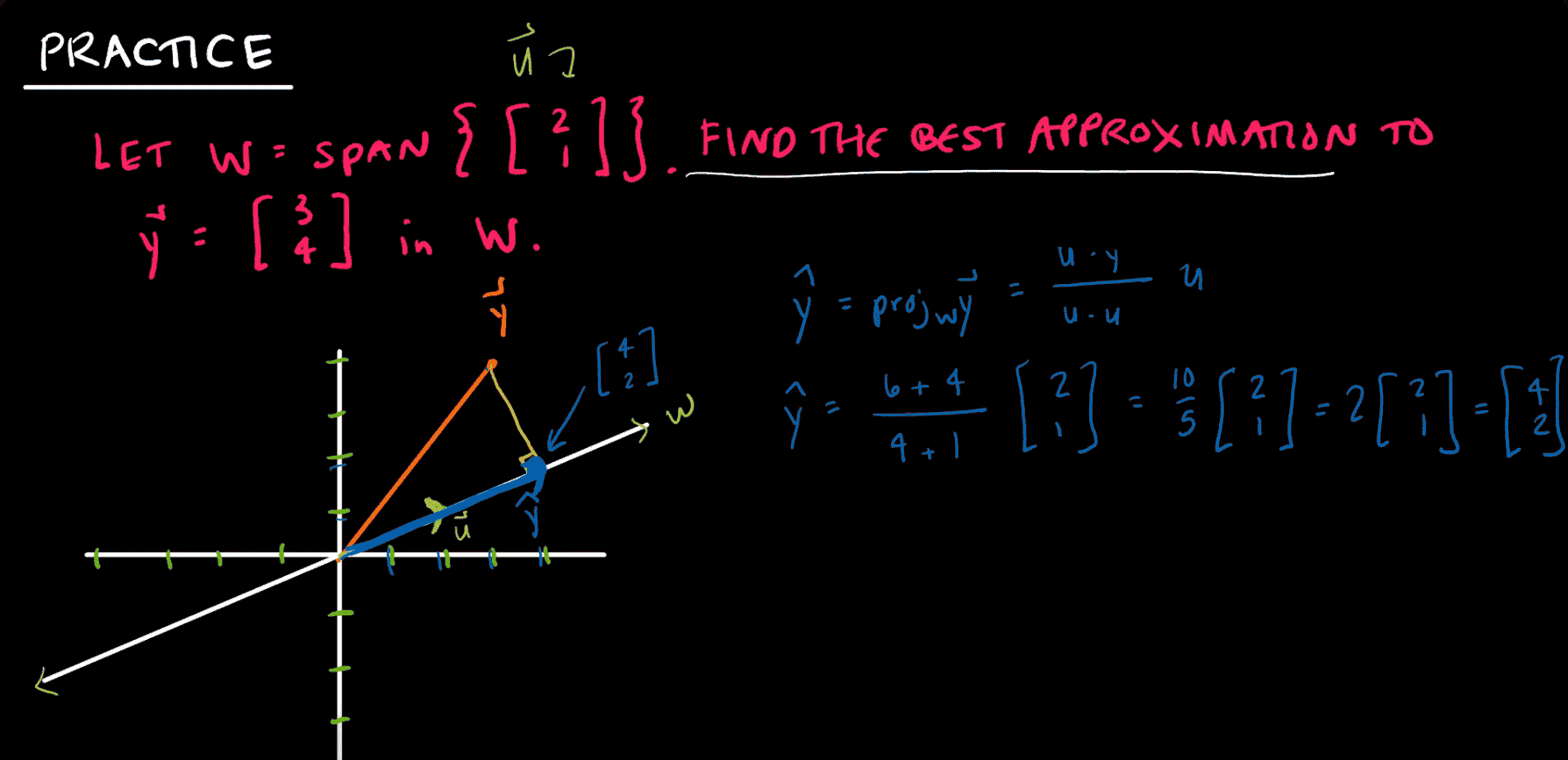
What is happening here, is you are projecting a vector on to a, or a series of basis vectors.
- You might be given those vectors, but you’ll most likely have to get them with G.S.
- “Those vectors” are the orthogonal basis
In a 3D space, you’ll have a bunch of those orthogonal basis’s
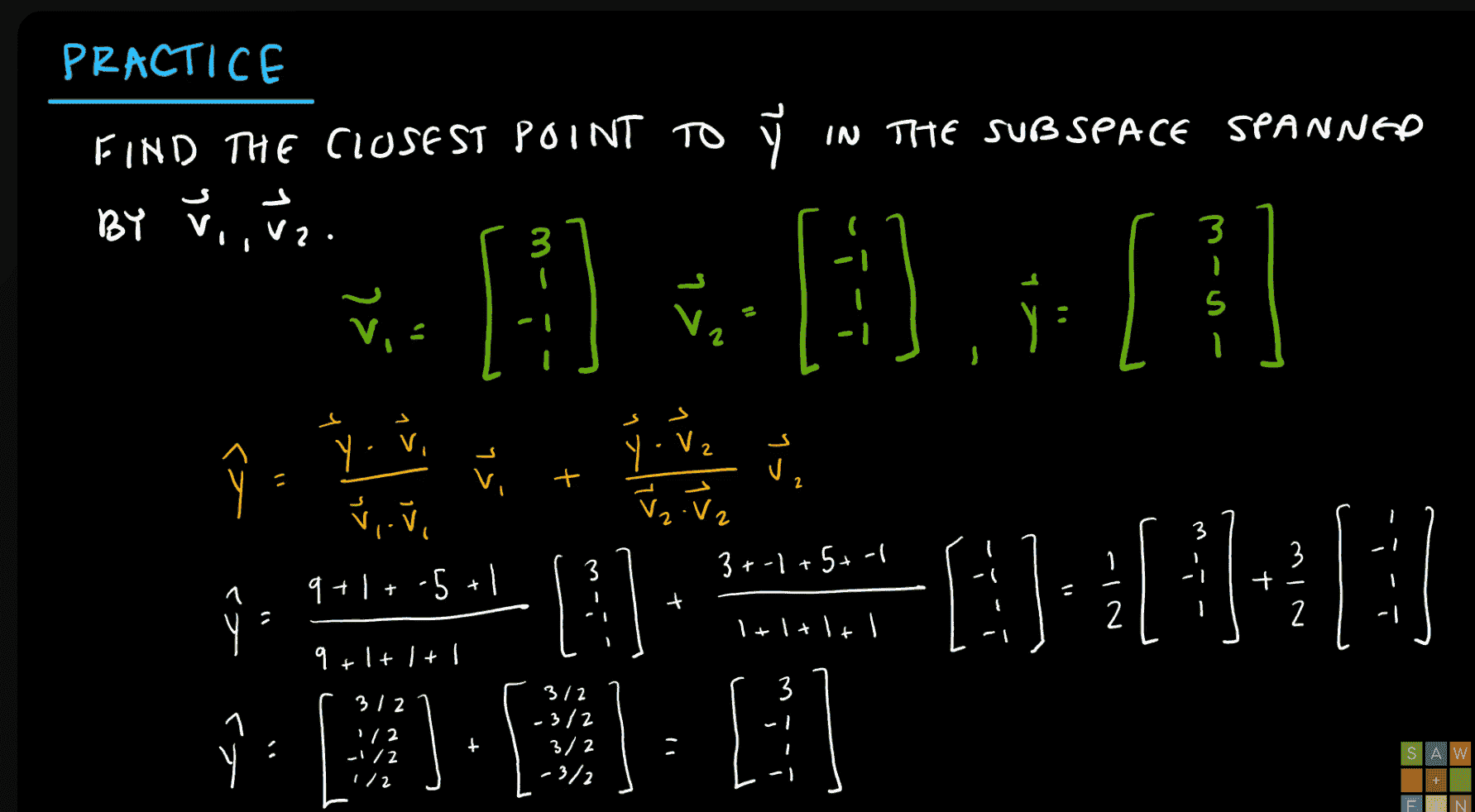
- Here, you can see what she is doing. In green she is defining her two basis vectors, and her other Y vector.
- In orange, she is setting up a projection formula for each basis vector, summing them up.
What you receive, is the best approximation of the subspace, or the closest point to the subspace.