Basis and Dimension

Basis

• Basis are the vectors which make up a dimension

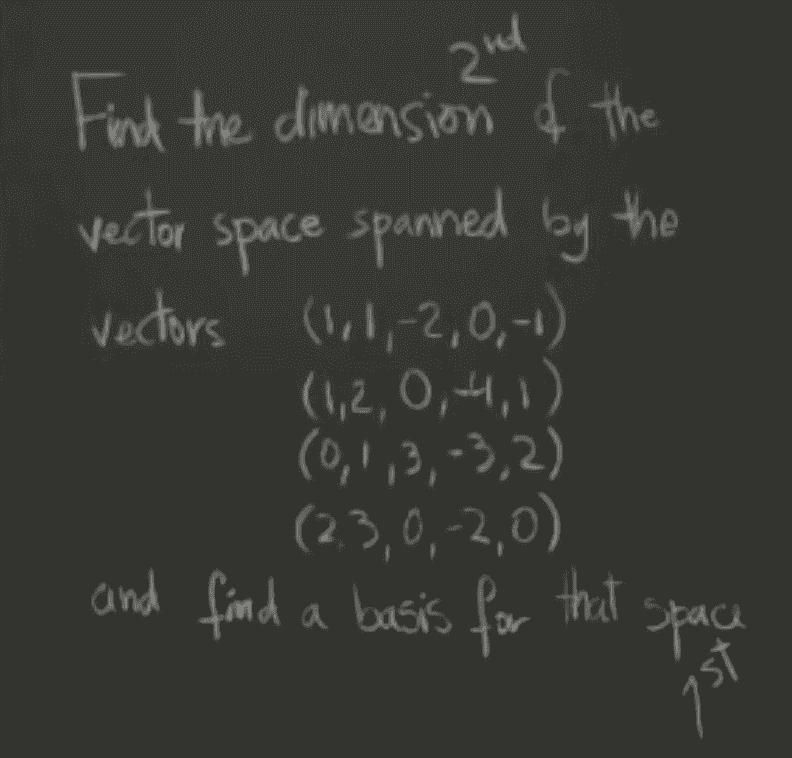
• If you are given a vector set, like this, you have to check for linear independence. Just because you have four vectors, doesn’t mean that one, two or even three could be dependent on the first.

• To solve for the basis vectors, or the ones that actually matter to the system, you have to do REF to see if you have a zero row.

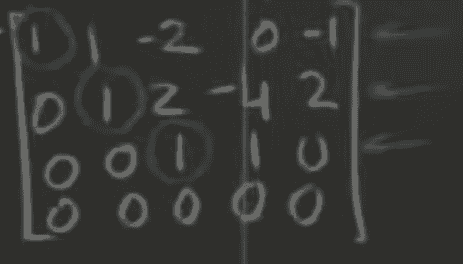
• So here, only the first three vectors matter (They are inserted by row here)

$$\left[\begin{array}{ccccc}1& 1& -2& 0& -1\\ 1& 2& 0& -4& 1\\ 0& 1& 3& -3& 2\end{array}\right]$$

As such!

• These are our basis vectors. The last one is dependent.

Row Space

• Row space is loading the vectors into the matrix by ROW and doing REF to find the amount of not zero rows

• The amount of pivot rows denote the amount of basis vectors.

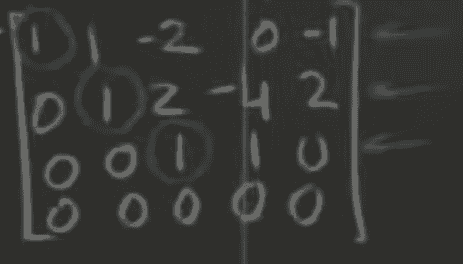
The example used just now was row space!

• The vectors given post REF are the basis for row space.

Column Space

• Row space is loading the vectors into the matrix by COLUMN and doing REF to find the amount of pivots

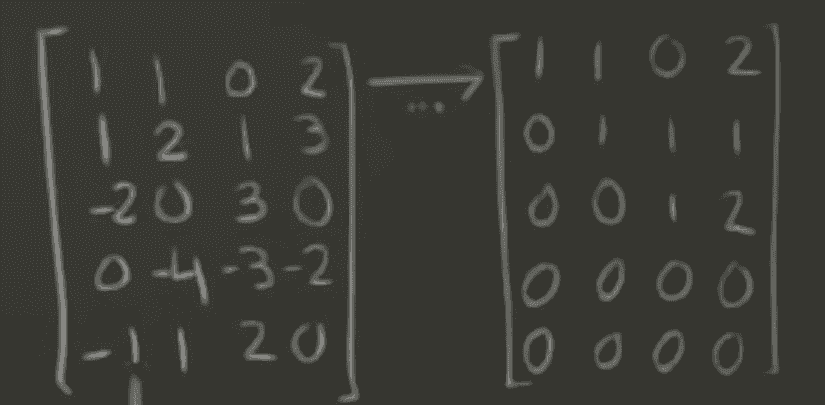
• Here! The final row does not have a pivot. Therefore, it is not a basis! ℝ³
• You must go back to the original vectors to give, as column space does not give REF’ed vectors.

---

Dimension

Dimension is easy! The dimension, ℝⁿ is defined by the number of basis vectors.