Combinations and Permutations

Counting Principles:

• Often outcomes are equilikely, but there are numerous possibles. How can we figure out the number of possible outcomes?

  • Can use a tree diagram, but usually takes FOREVER, especially with a large initial set
  • 

• We can use what’s called the Multiplication rule to speed things up.

Multiplication Rule

If an experiment has k stages, and

1. Stage 1 has m₁ possible outcomes,
2. Stage 1 has m₂ possible outcomes,
3. …
4. Stage K has m_k possible outcomes,

then the total number of possible outcomes is

n = m₁ * m₂ * … *m_k

Usually, one sets it up like this using dashes

$$\underline{2}\underline{2}\underline{2}\to 8$$

---

Example 1

Total outcomes are n = m_k, The second half is an aside.

It turns out, the probability of each outcome occurring is

$$\frac{1}{m^k}$$

Pretty low right?

---

Example 2

a) How many ways can 6 unique people line up?

$$\underline{6}\underline{5}\underline{4}\underline{3}\underline{2}\underline{1}\to n=6(5)(4)(3)(2)(1)=6!$$

6!, or about 720 unique ways.

b) Two people are friends, and want to stand to stand together in the line up

$$(\underline{5}\underline{4}\underline{3}\underline{2}\underline{1})\times 2\to 240$$

c) Two people have a fight and now refuse to stand next to each other in the line up.

720 is the total number of ways that these two can be together, and not together. Here, we already know the total amount of ways that they are together, that being 240.

so…

$$n=720-240=480$$

So the answer is 480 distinct ways.

---

Special Cases

• Permutations:
  • An arrangement of distinct objects, where order matters (ex, “ab” versus “ba”)
  • If r objects are selected from m objects, then the number of permutations is

$$n=\frac{m!}{(m-r)!}=P_r^m$$

In the case of our six person line up from earlier, the order mattered. (ie, who wants to be in line first, etc) In that case,

m = 6 r =6

$$n=\frac{6!}{(6-6)!}=\frac{6!}{0!}=\frac{6!}{1}=6!=\underline{720}$$

---

Example 3

Consider the four letters a,b,c and d.

a) What are all the permutations of these letters taken at a time?

m = 4 r = 1

$$n=\frac{4!}{(4-1)!}=\frac{4!}{3!}=\underline{4}$$

b) What are all the permutations of these letters taken two at a time?

m = 4 r = 2

$$n=\frac{4!}{(4-2)!}=\frac{4!}{2!}=\frac{4\times 3\times 2\times 1}{2\times 1}=4\times 3=\underline{12}$$

What are they?

		ab ba
		ac ca
		ad da
		bc cb 
		bd db 
		ad cd

n = 12.

---

• Combinations: ^8b383e
  • An arrangement of distinct objects where order does not matter.

$$n=\frac{m!}{(m-r)!r!}=\text{m}\underline{choose}\text{r}$$

---

Example 4

How many combinations can we have choosing two letters from a,b,c and d?

m =4 r=2

$$n=\frac{4!}{(4-2)!2!}=\frac{4\times 3\times 2\times 1}{(2\times 1)(2\times 1)}=\frac{4\times 3}{2\times 1}=\underline{6}$$

---

Example 5

A company keeps a list of eight software suppliers. Not all suppliers are asked to provide a quote on a given request. Determine the number of ways 3 suppliers can be chosen from the list.

m = 8 r =3

We have determined here that order does not matter. It doesn’t matter in which order we choose the suppliers. We can use a combination here

$$n=\frac{8!}{(5!)3!}$$

Incomplete! He has it in his notes, I could not finish it.

---

Example 7

Suppose you have been dealt (randomly) 13 cards from a bridge deck. What is the probability that they are all spades? What interpretation did you use to access this probability?

Now,

m = 52 r = 13

Does order matter in this case? No.

$$n=\frac{52!}{(52-13)!12!}=\frac{52!}{39!13!}=52\times \mathrm{51...}\times 41!\times 4013\times 12\times ...\times 2\times 1=\underline{635,013,559,598}\approx \underline{6.4\times 10^{11}}$$

So the probability of you getting 13 spades in a row is

$$\frac{1}{6.4\times 10^{11}}$$

That’s a pretty low chance!!

Note

The total possible sets of 13 cards randomly is 635,013,559,598, or 6.4x10¹¹

---

Mathematics of Probability

How do we compute the probability of an event?, P{events}

We start with 3 fundamental assumptions that have been studied in Statistics for centuries.

1. P{A} ≥ 0

2. The certain event, P{s} = 1
   Probability is a number between 0 and 1 that says how likely something is to occur: 0 means it’s impossible. 1 means it’s certain.

3. For any sequence of disjoint events, the probability of their unions, is just the sum of their probabilities. or

$$P(A_1\cup A_2\cup ...\cup A_n)=P(A_1)+P(A_2)...P(A_n)$$

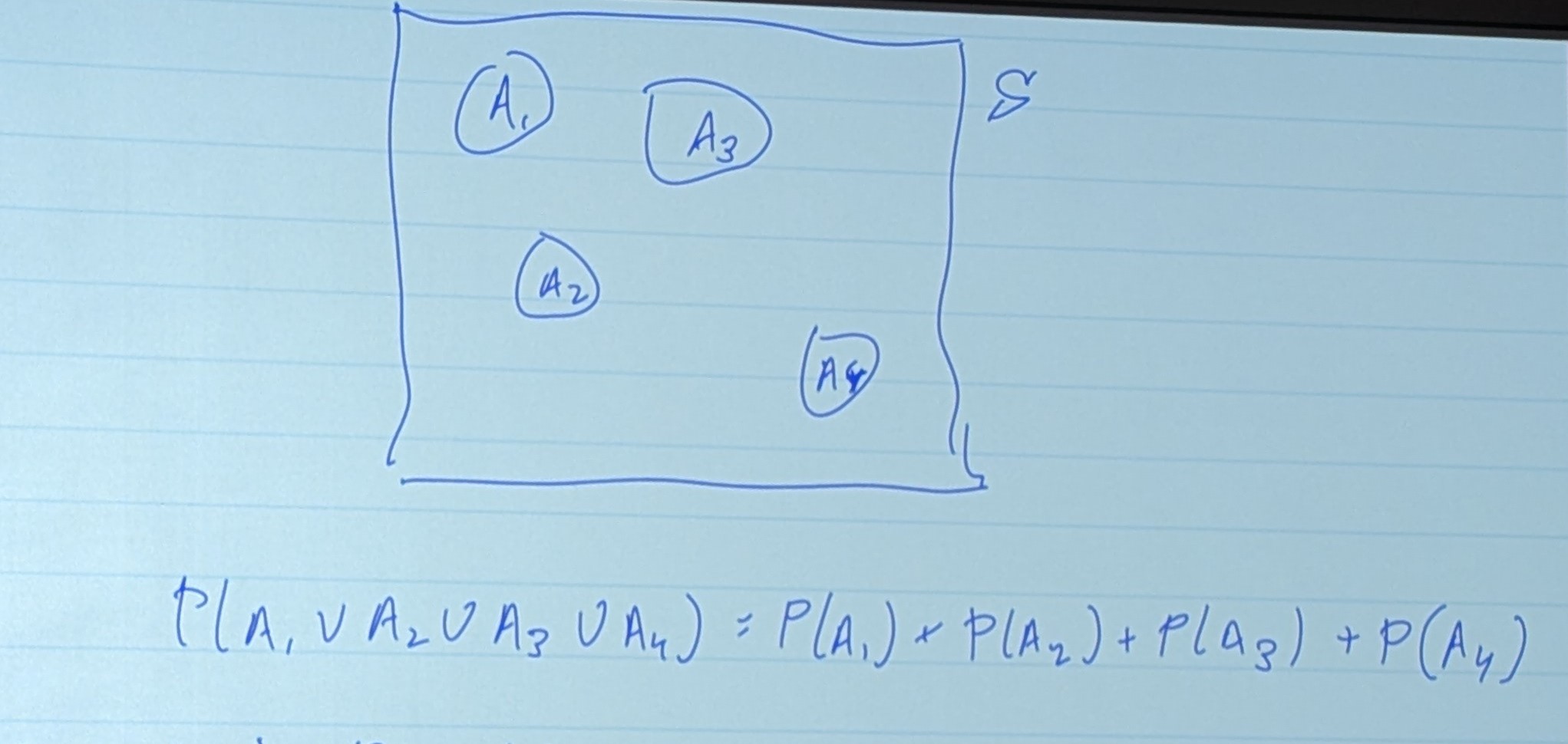
Here are some important results…

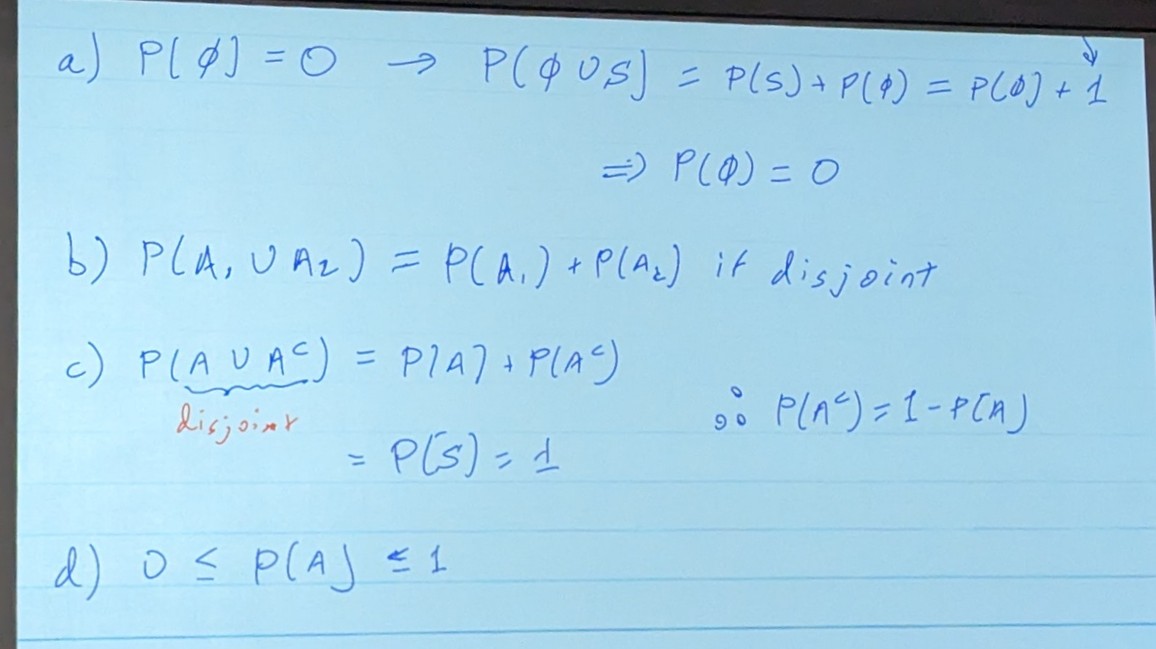
e) for any two events

$$P(A\cup B)=P(A)+P(B)-P(A\cap B)$$

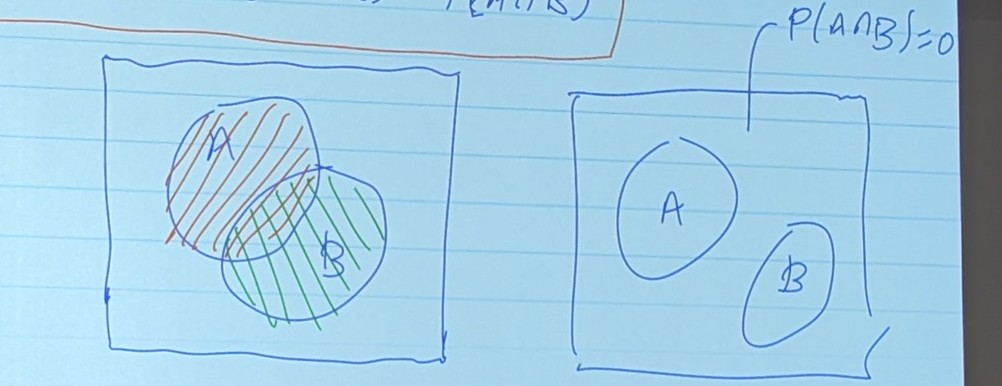
If we have three, or more events,

You’ll want to add all the probabilities of each, and subtract the intersections

This is the general case

---

However, if they are disjoint!! (I,e not overlapping on the Venn diagram ) It makes life a whole lot easier.

$$\text{If disjoint},P(A\cup B\cup C\cup D)=P(A)+P(B)+P(C)+P(D)$$

This will save you a lot of time.

---

In the thick of it, you will probably want to refer to probability using the number over 100 (i,e 0.82, or 0.54) instead of percentages (i,e 82% or 54%), like you’d usually hear when discussing probability.

It makes things much easier to add, and multiply.