Implicit Functions and Differentiation

Explicit Functions: y=F(x)

Implicit Functions: F(x,y)=0

• All X’s and Y’s are on one side!

• Explicit functions can always be written as implicit functions

• When looking for the rate of change of an implicit function, we have to to implicit differentiation

Implicit Differentiation

Example

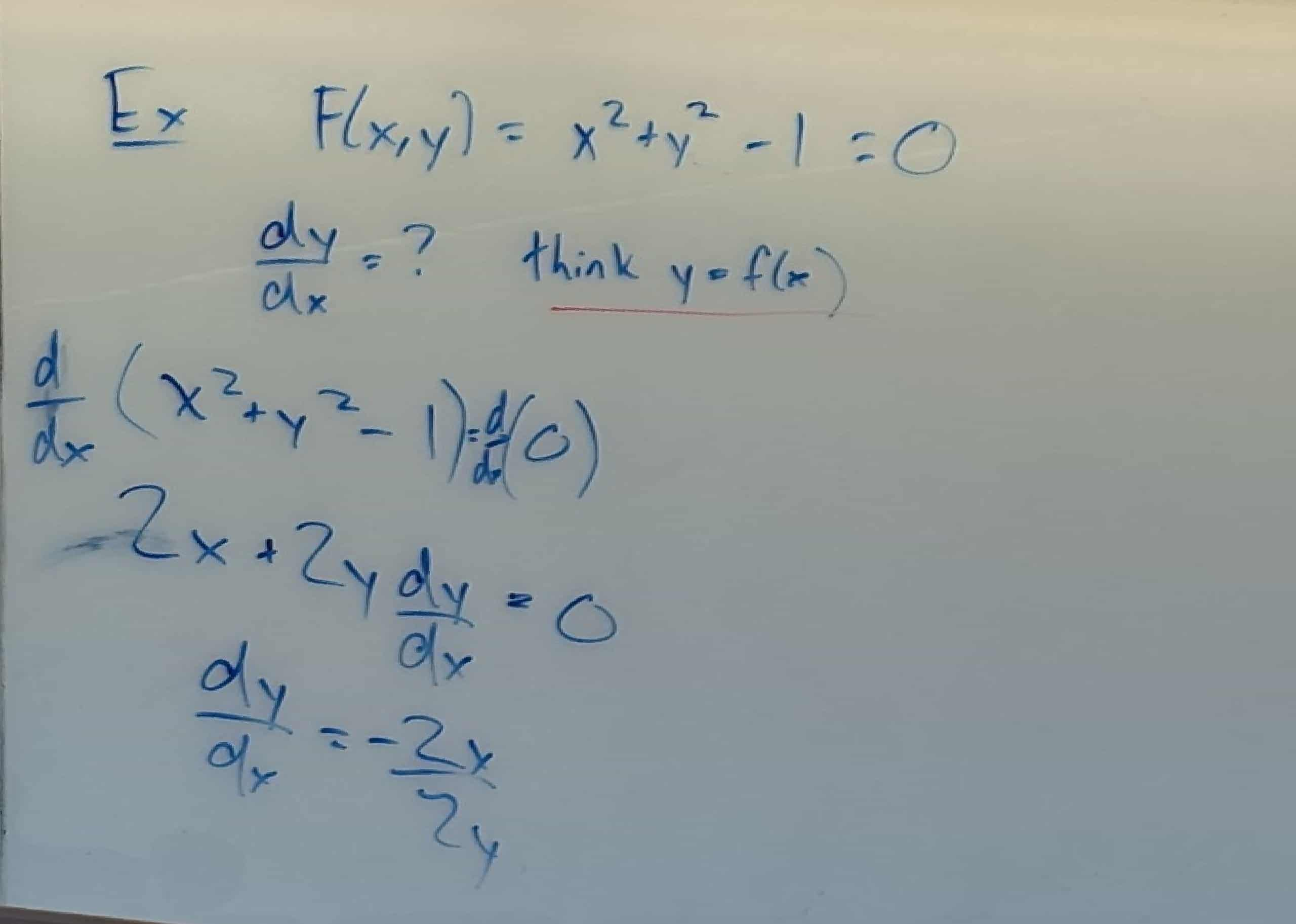
Remember, that y=f(x), or whatever term you are differentiating in terms of.

• Where we are differentiating by dx, Y acts as a functions f(x).
• From there, we chain rule our f(x) function, by derivative of outside times derivative of inside

---

Example

• Here, look at the tree!
• F is a function of x, y and z
• X stands on its own (first term)
• Y does not depend on X! So it has zero rate of change (second term)
• Z depends on both X and Y, but we are differentiating in terms of X, so it’s all we care about! (Last term)
• Re-arrange and solve for dz/dx!

Example to try for later!

$$z^{2}y+3y^{2}x-4x^{3}z=0$$

• Solve for (dx/dz)

---

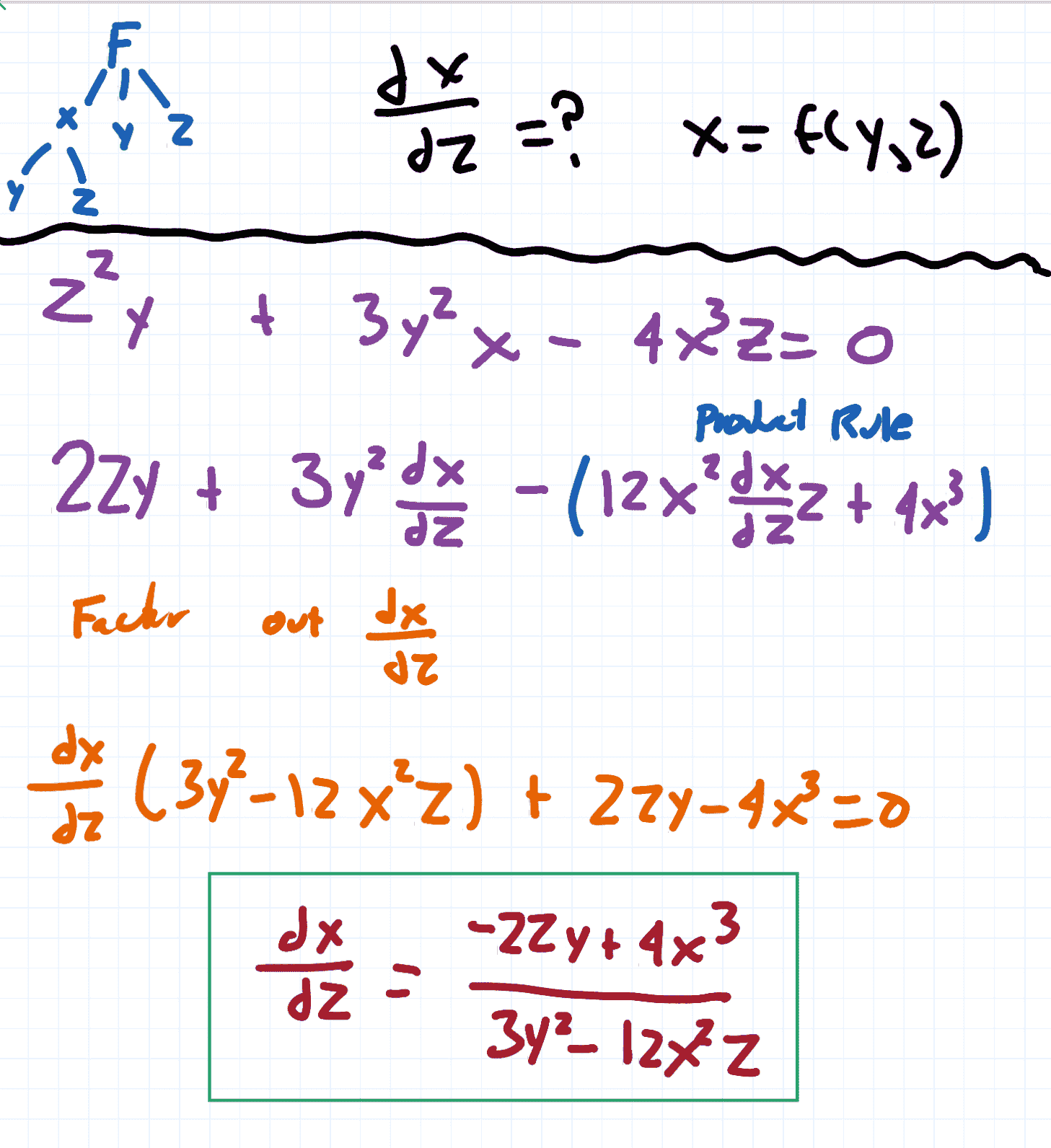
Gradients and Directional Derivatives

Gradients

• Gradient of a function is a vector whose components are partial derivatives!

${\nabla }_f$ (The upside down triangle is known as the “nabla”, which is the gradient of F)

2D

$$f(x,y)={\nabla }_f=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y})$$

3D

$$f(x,y,z)={\nabla }_f=(\frac{\partial f}{\partial x},\frac{\partial f}{\partial y},\frac{\partial f}{\partial z})$$

Example

w = f(x,y,z) = xy +cos(z)

$${\nabla }_w=(\frac{\partial w}{\partial x},\frac{\partial w}{\partial y},\frac{\partial w}{\partial z})$$ $$=y,z,-sin(z)$$

Directional Derivatives

• Rate of change of F in a direction of û
• û can be anything chosen!

$$D_{u}f\text{ if }\hat{u}=\hat{i}\Rightarrow D_{u}f=\frac{\partial f}{\partial x}$$

Generally,

$$D_{u}f={\nabla }_f\cdot \hat{u}$$

Example

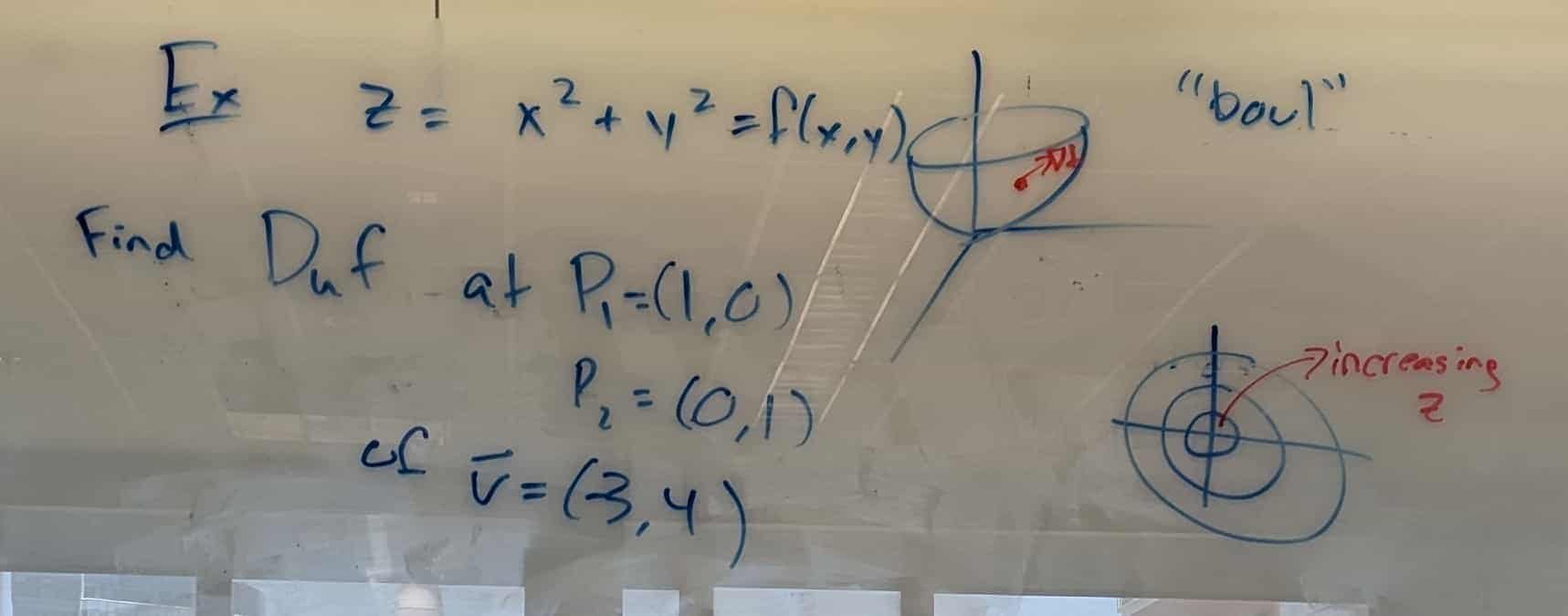
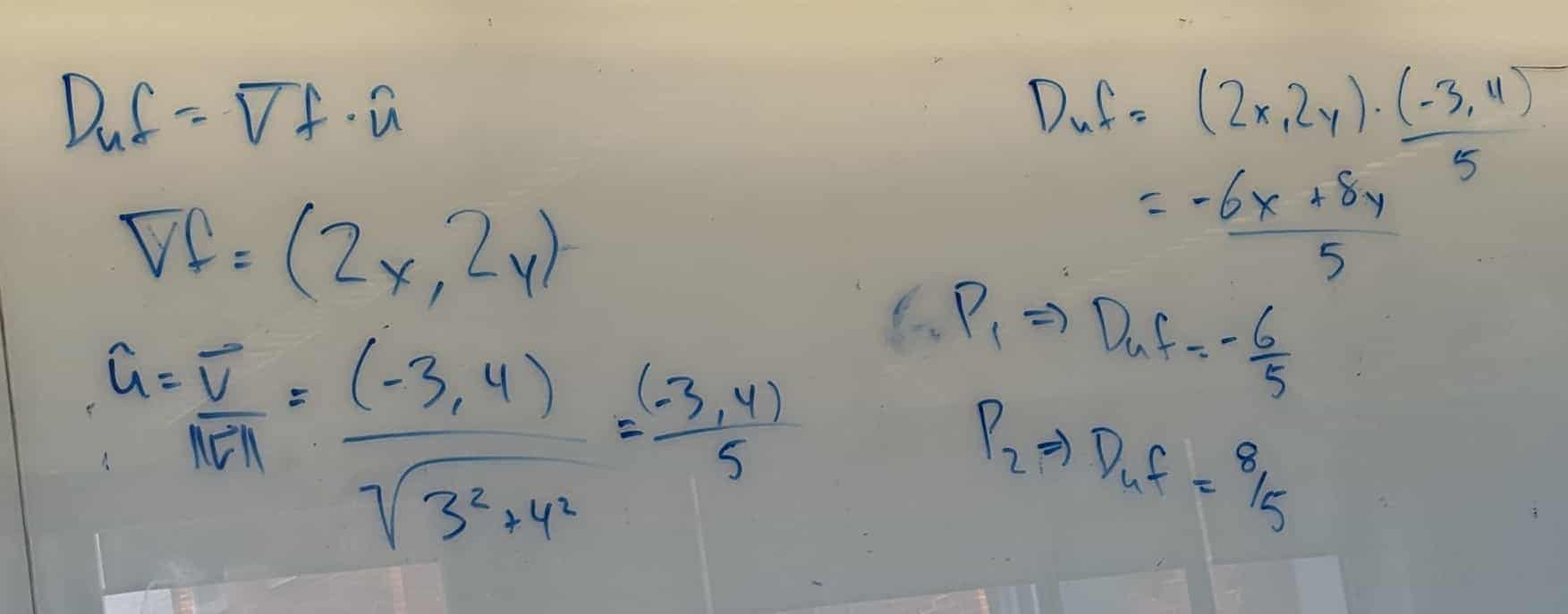
• Gradients are perpendicular to your level curves, and point to higher levels!
  • Unless the directional derivative is NEGATIVE. It then means you are pointing downwards
  • Which in this case, -(6/5)^th is.

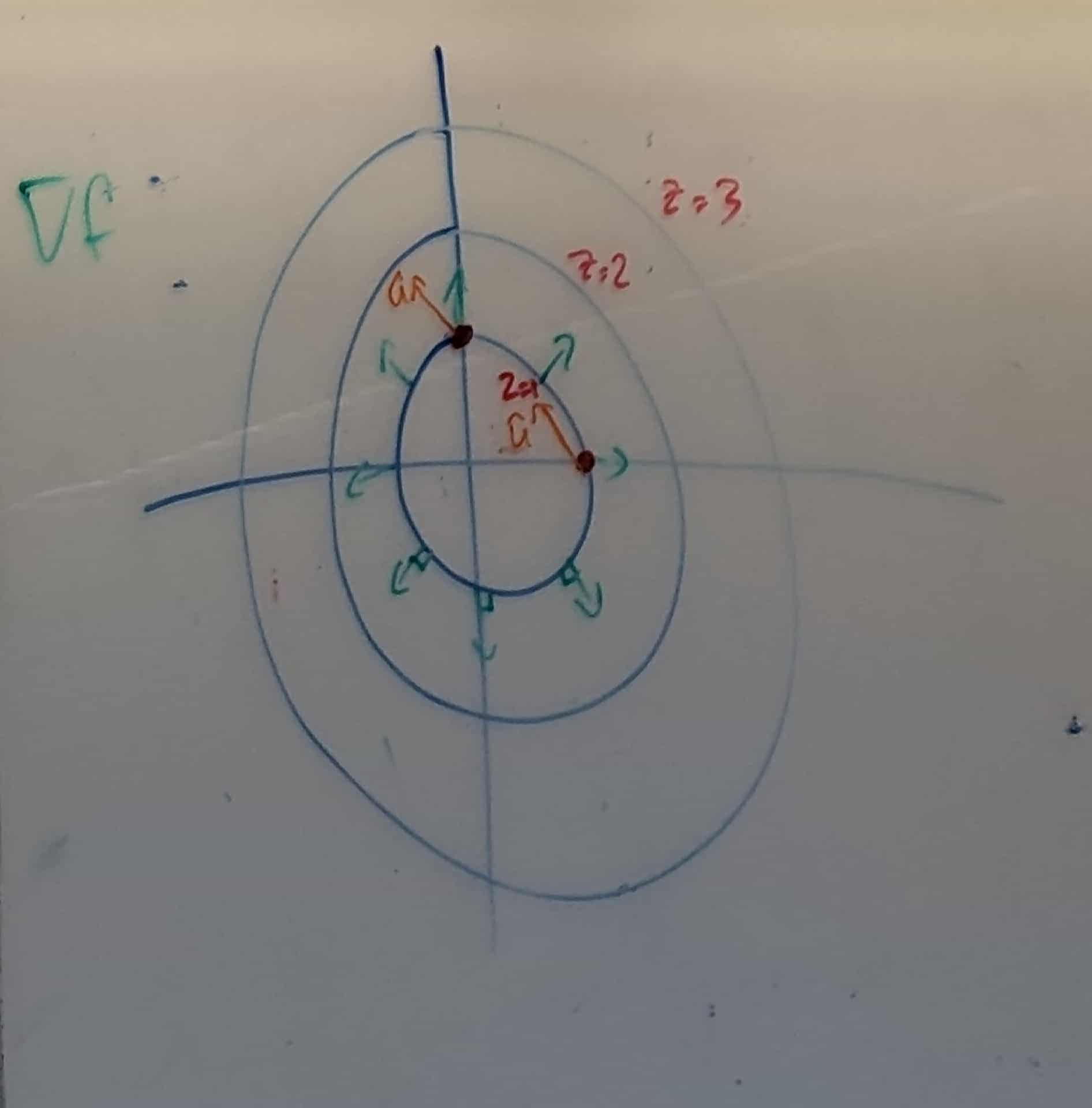
Here’s a slightly squished graph of that problem!

• Blue lines are the level curves lines
• Green lines are the upwards gradient lines
• Orange arrows are the û vectors calculated

Some quick questions about it..

1. What is the direction of steepest ascent here? Parallel to the gradient, going upwards! Direction of gradient ➟ (2x, 2y) I’m at (1,1) ➟ (2,2)

2. What is the direction of steepest decent here? Antiparallel to the gradient, going downwards! Direction of gradient ➟ (-2x, -2y) I’m at (1,1) ➟ (-2,-2)

3. What is the direction of no ascent or decent here? Perpendicular to gradient tangent to level curve $\hat{u}\cdot \nabla f=0$ You’ll have F, and you’ll need to solve for û

The equation of a plane that contains the point (x0,y0,z0) with normal vector →n=⟨a,b,c⟩ is given by,

a(x−x₀)+b(y−y₀)+c(z−z₀)=0