Linear Combination
-
A linear combination is something you can make by adding scalars to each of the given vectors, and adding them up.
-
The sum of all vectors, with a scalar
-
That’s all!
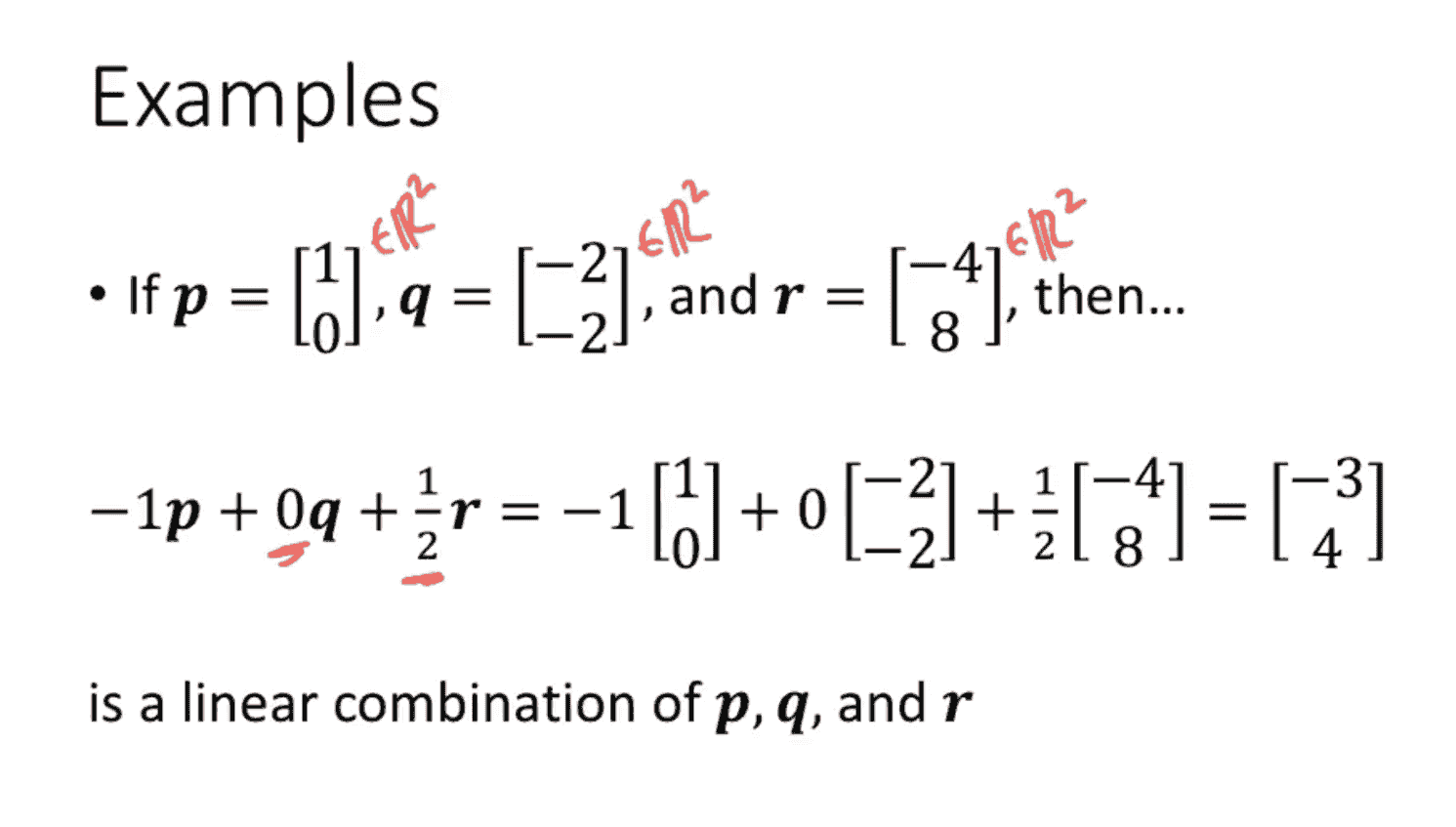
Span
- The span is the area that can be reached by any linear combination
For a non zero single vector, the span would look kind of like this
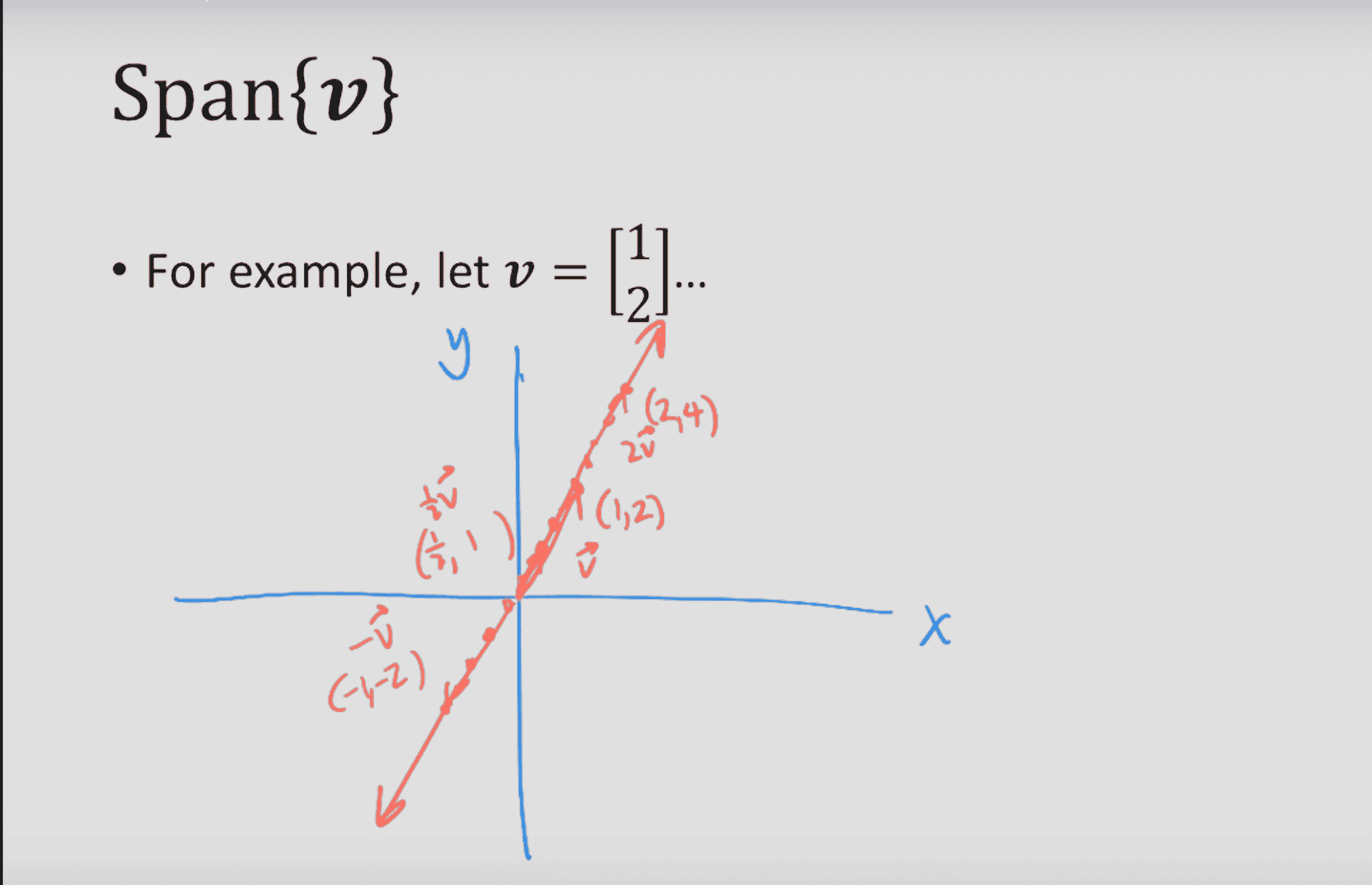
- The span is anywhere that this line can get too! There’s only a single vector here.
Here, we’ve got two vectors.
- Two vectors are usually visualized as a plane, as with giving those two vectors scalars, you can get anywhere on that plane.

This can go on, and on and on… for n vectors (meaning it can be in ℝn)
- Sometimes, “span” can be a verb, and it can “span ℝn”.
- That would mean that the span of the set of given vectors covers everywhere in that dimension
Linear Independence
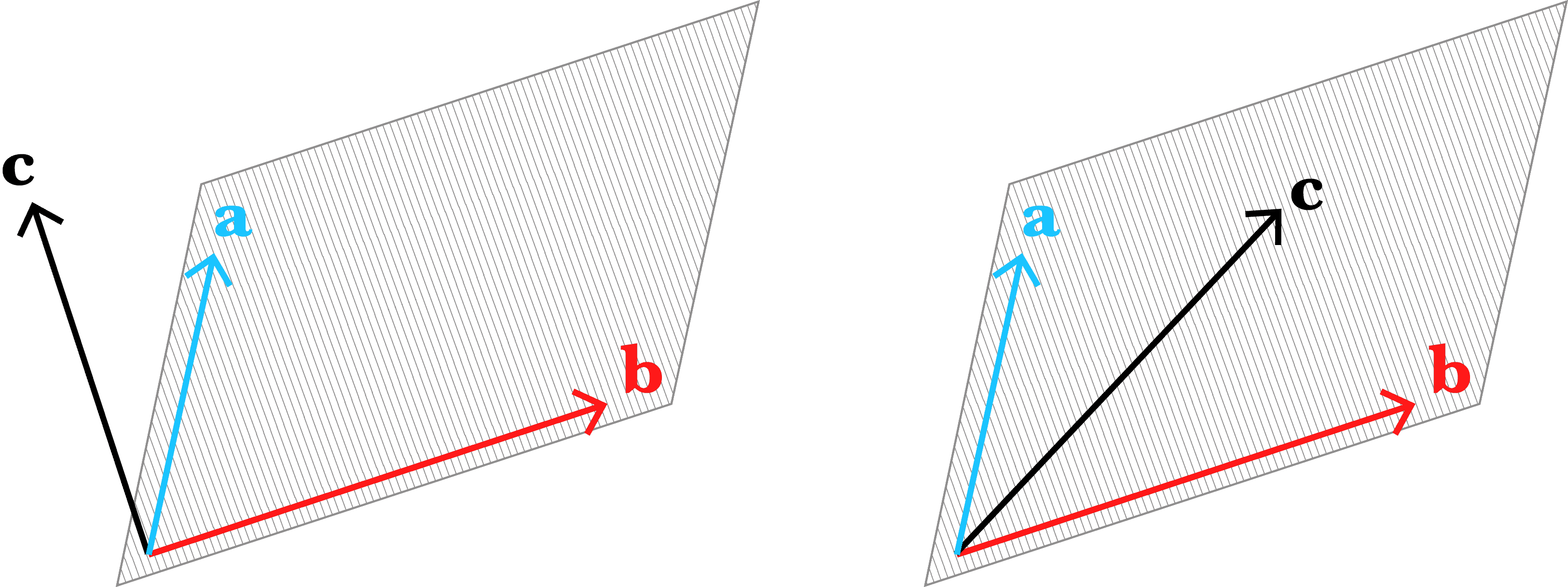
- Any set is linearly independent If no element in the set is a linear combination of other elements in the set.
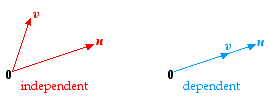
Example of Dependence
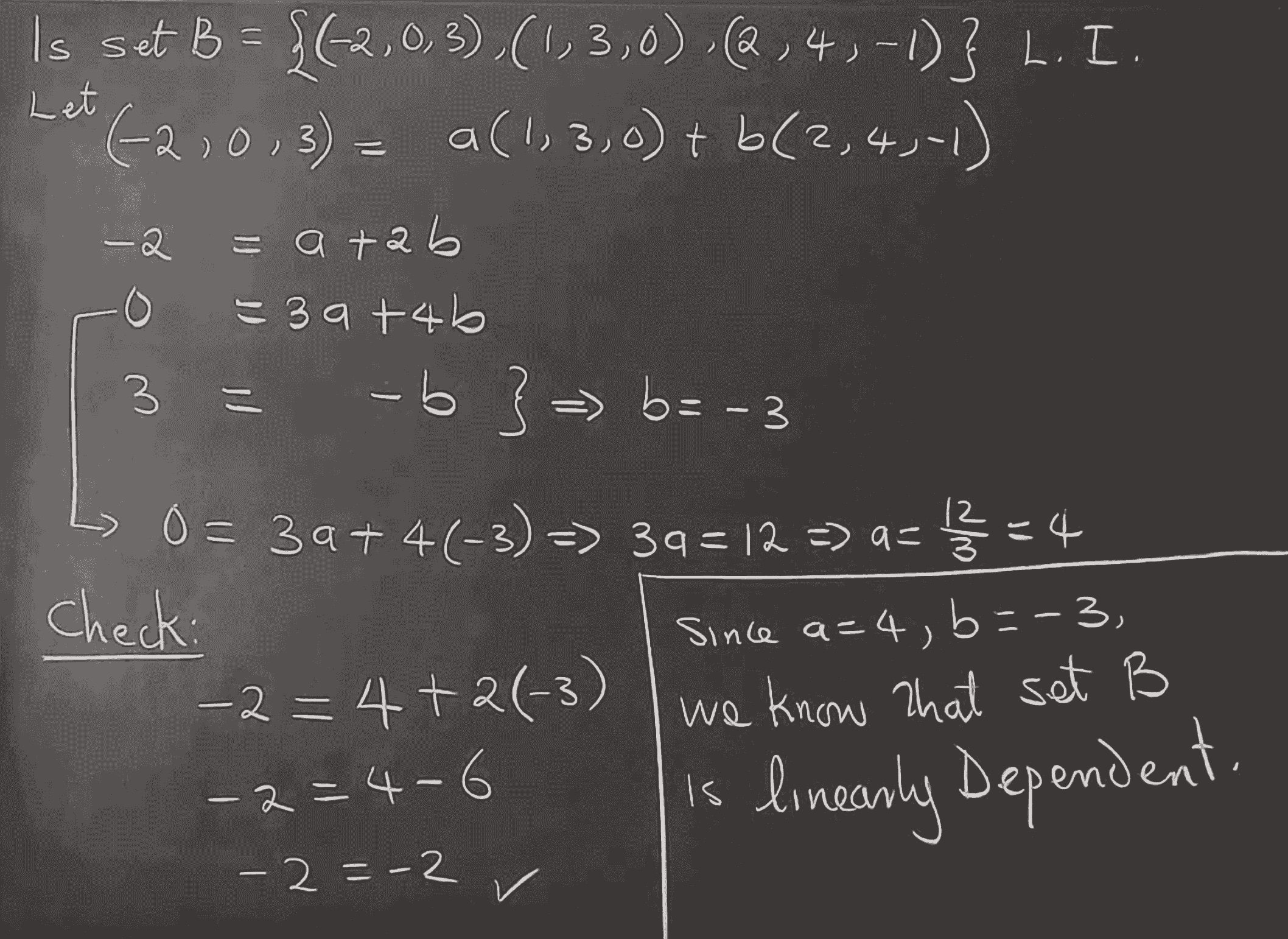
Example of Independence
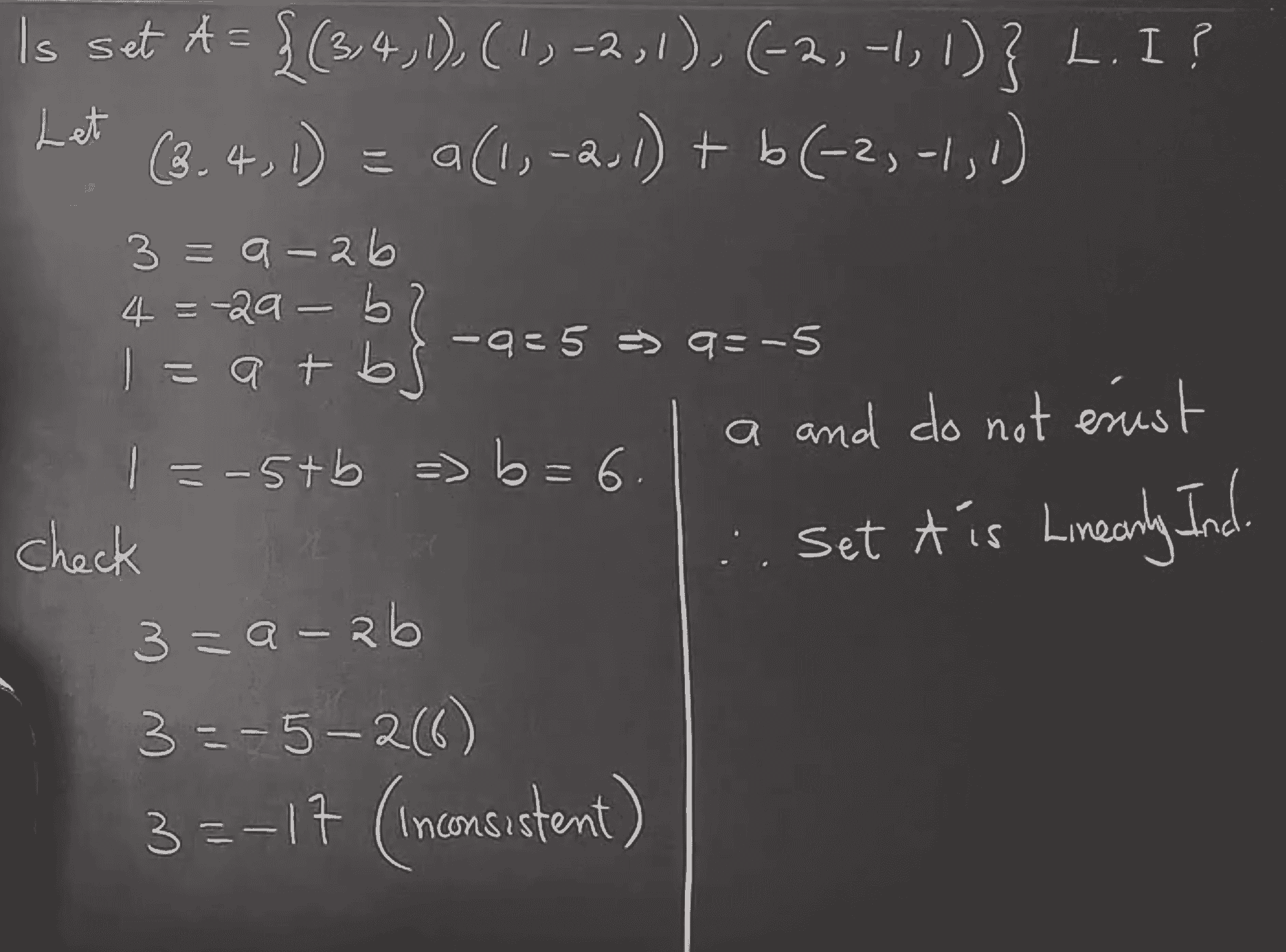
What can also be done to solve for linear independence/dependence is:
- Put vectors into a matrix
- Do RREF
- If there is a row of zeros, you now have a “free parameter” and you have linear dependence.
Examples of 2D and 3D linear dependence and dependence!