Orthogonal Sets in Rn

To begin, it is important to know that “Orthogonal” just means to be perpendicular to something.

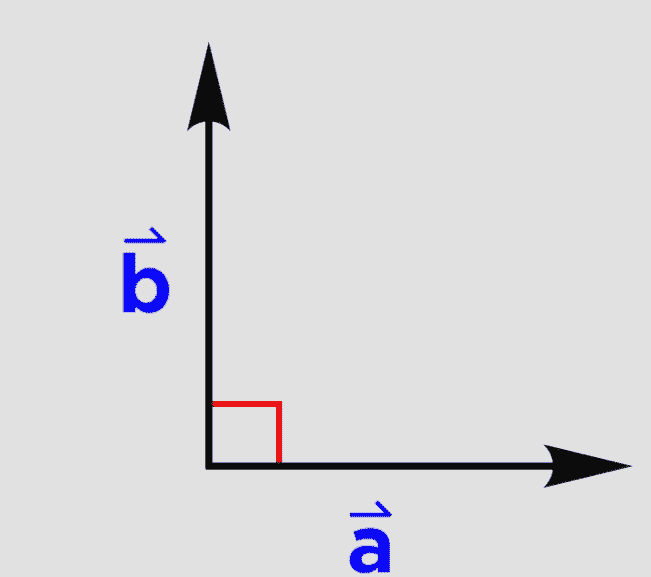
• Here, b̂ and â are orthogonal, perpendicular!

To check if two vectors are orthogonal, one can take the dot product.

• If the dot product does not equal zero, well… b̂ and â aren’t orthogonal
• However, if it does, then b̂ and â are orthogonal!
• This occurs, because the cos term in the dot product operation is at 90°. Cos(90) = 0

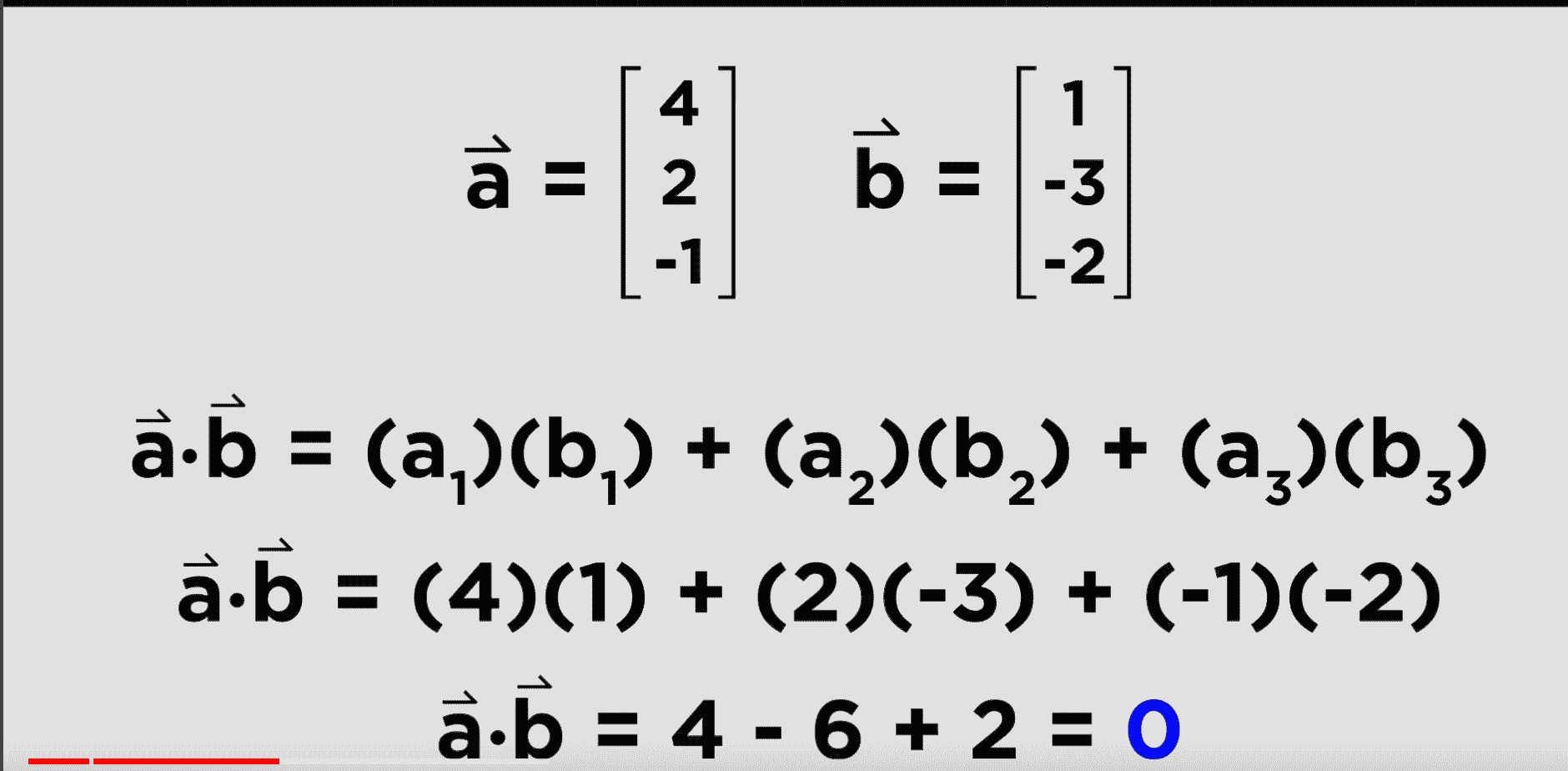
• Here is an example where that is the case!

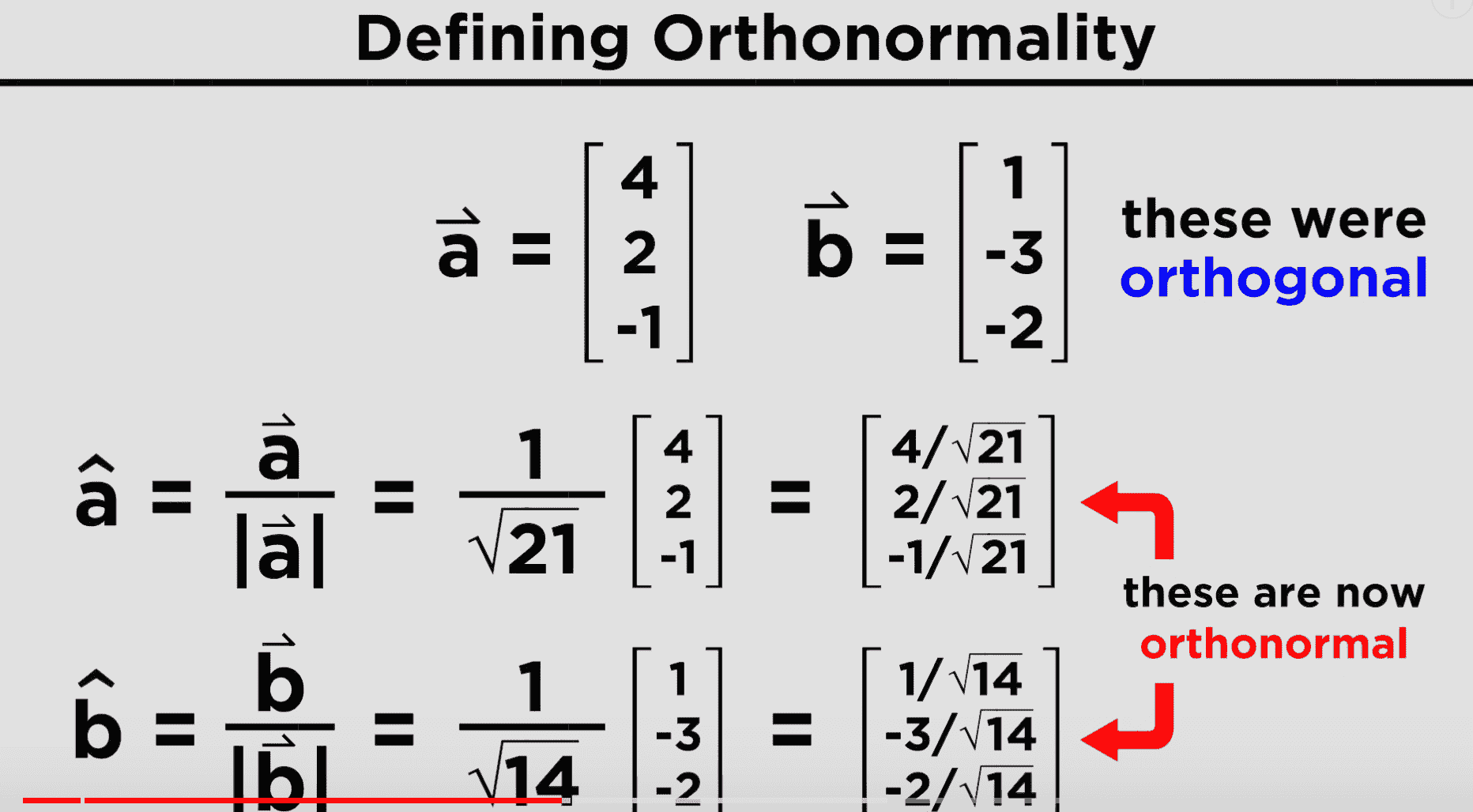
Orthonormality

If vectors b̂ and â are:

1. A unit vector (length of 1)
2. Orthogonal

They are what is known as orthonormal

• A reminder, to get the unit vector, it is the vector divided by its magnitude

$$\frac{\vec{a}}{\sqrt{\overrightarrow{a^2}}}=\hat{a}$$

• Example!

---

Now, you can also have spaces that are orthogonal to each other.

• Pretty cool!

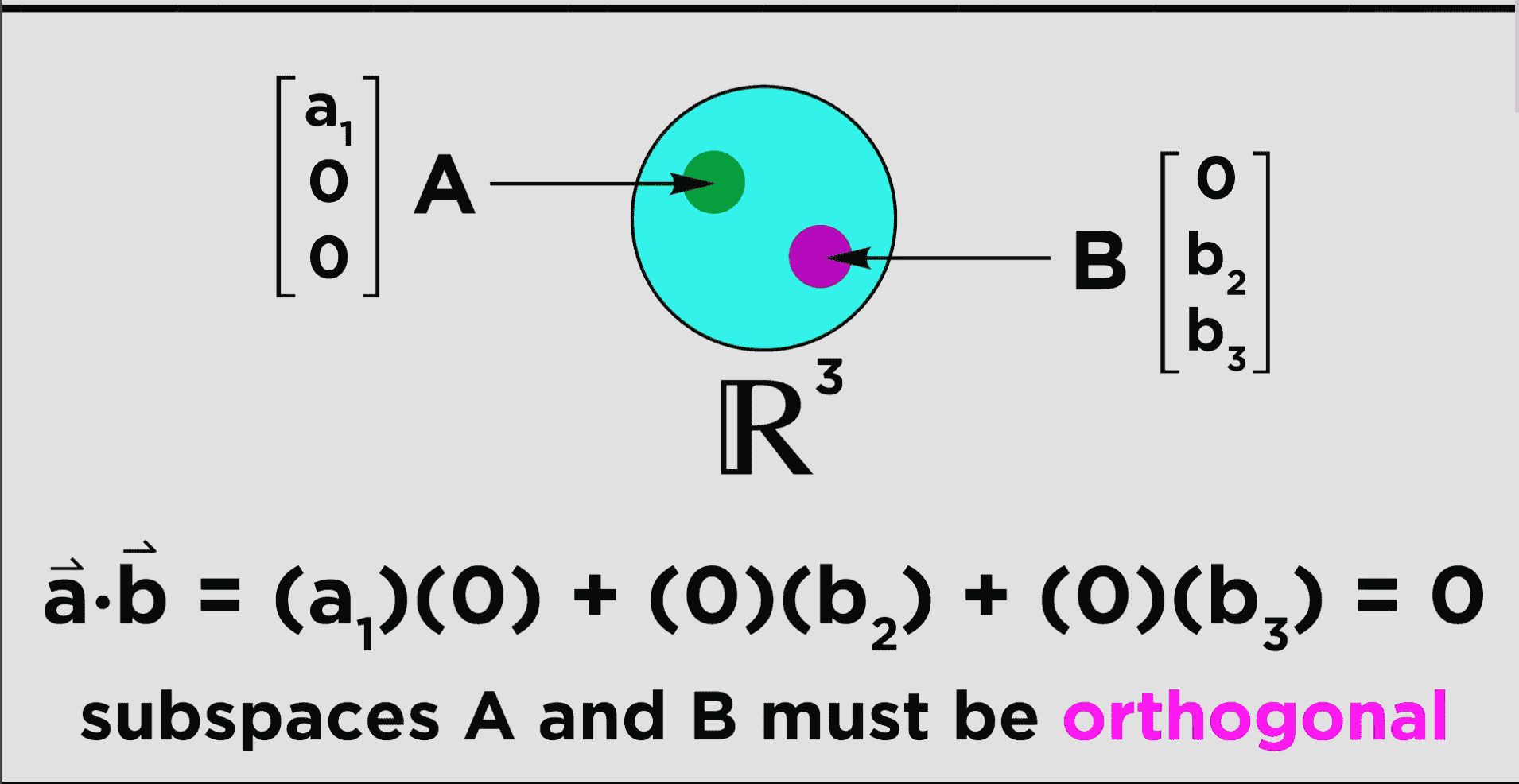
What is happening here, is that we have a subspace A and a subspace B

• Subspace A is only taking up the first row of the vector defining the space.
• Subspace B is only is only taking up the second and third row of the vector defining the space.

So, if we take the dot product of the b̂ and â vectors making up A and B, as Dave does here, we will get zero!

• If you remember from before, this makes them orthogonal!

—

Orthogonal Square Matrices

You can also check to see if square matrices are orthogonal

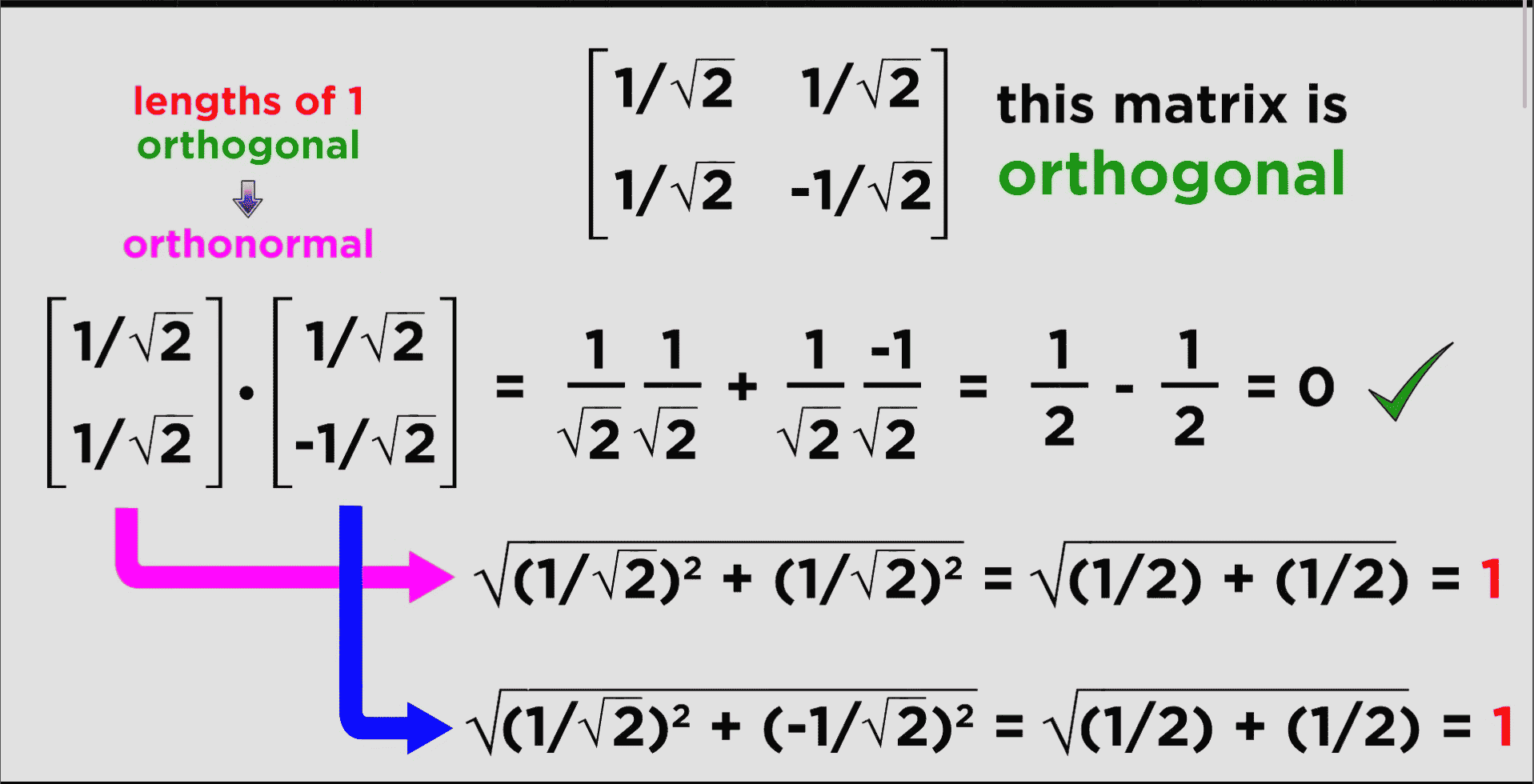
• This involves taking the dot products of each vector put into the matrix, and ensuring that they are orthonormal (i.e. length of one, and orthogonal (dot product equals zero)

Orthogonal Sets

An Orthogonal Set is pretty easy.

• An orthogonal set is a set of vectors (two or more), that are all orthogonal!

*some steps skipped here, but each row is being multiplied, then they are all being added (dot product)

Every single vector has to be orthogonal to each other, with no exceptions

• In this case, V₂ and V₃ failed, even if the rest are good, this is not an orthogonal set.

• Get the idea?

What you are REALLY here to see

• Well, that’s cool and all, but what is the point in finding all of this?
• The reason why is pretty unique, and quite helpful.

For an orthogonal matrix (A) its inverse (A^-1) is simply the same as its transpose (A^T)

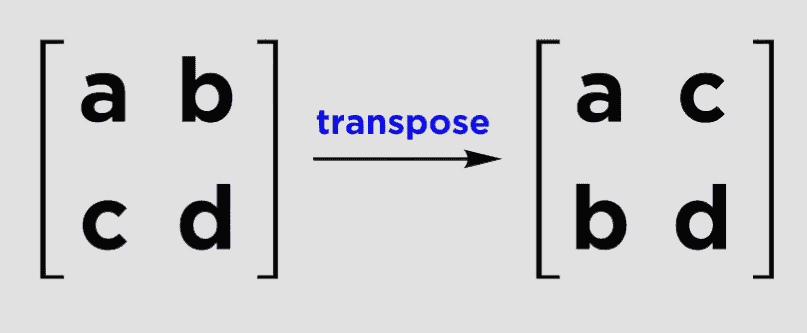
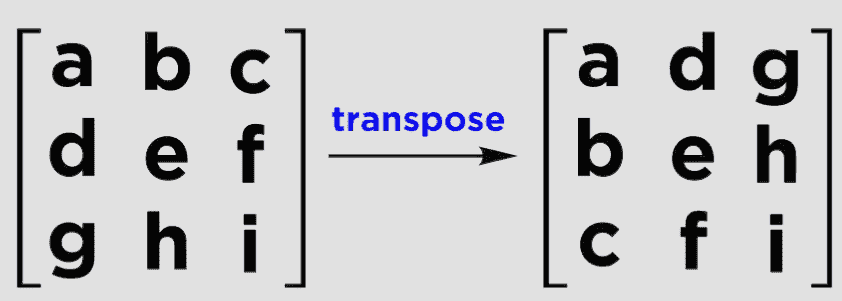
• This makes it REALLY easy to find the inverse of an orthogonal matrix, quickly. You can just make the columns the rows, and the rows the columns

— Last topic for Orthogonality!

Another cool thing you can do, is find the orthogonality of functions

• This is done by defining a new operation known as the inner product

Given f(x), and another function g(x), from a point a to a point b ~

• The operation looks like this

$$<f,g>$$

• <f,g> is equal to the integral of *f(x)g(x) from point a to b

$$<f,g>={\int }_a^{b}f(x)g(x)dx$$

• Cool stuff!

• Now, if this inner product is = 0, then the functions are orthogonal over the range a to b

Example!

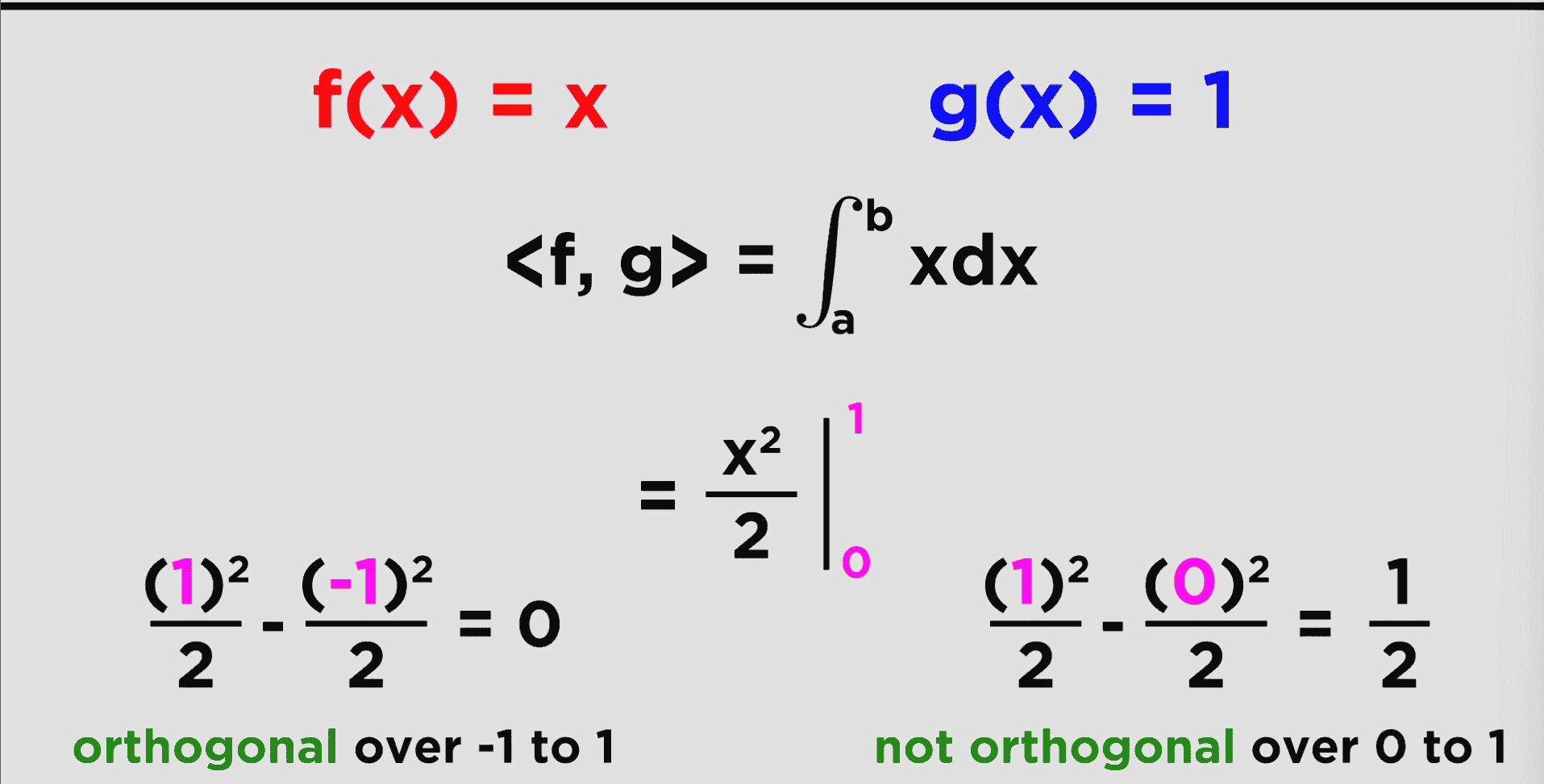
• Here, f(x) and g(x) are orthogonal over the range of (-1 to 1), but not (0 to 1)

---

Wrapping up here, but as a hint for later, another w(x) function can be thrown in here (weight function) to vary things up.

We will see this later!!!