Continuous Distributions

A continuation of Bernoulli Trials!

Exponential Distribution (This is our first continuous distribution)

Let T₁ = time until the next “success”

Distribution? CDF:

$$P[T_1<t]=P[N_t\ge t]$$ $$F_{T1}(t)=P(T_1<t)=1-P(N_t=0)$$

Exponential Distribution

There is a proof to say

Exponential Distribution

A reminder of the standard deviation (σ__T1)

$$\sigma =\frac{1}{\lambda }$$

Because variance is that with a lambda squared!

---

Gamma Distribution (analogous to the negative binomial)

Let T_k = Time to the K^th success

Gamma Distribution

There is a proof to say, that

Gamma Distribution

As before, PMF is integrated PDF

Looking at the CDF (Big F function), we can see that the higher the K value we have, and more T₁ terms we are going to have stretching out the function.

This is another interpretation of, let’s call it T₃, or the span of the whole time period. T₁ being the time in between each time period.

---

Memoryless Property

• Since every trial is independent of all other trials, the past is forgotten

---

Other Continuous Distributions

Weibull Distribution

• The Weibull distribution is a generalization on the exponential distribution
• It is a very common lifetime model distribution, or “time to failure” of a system

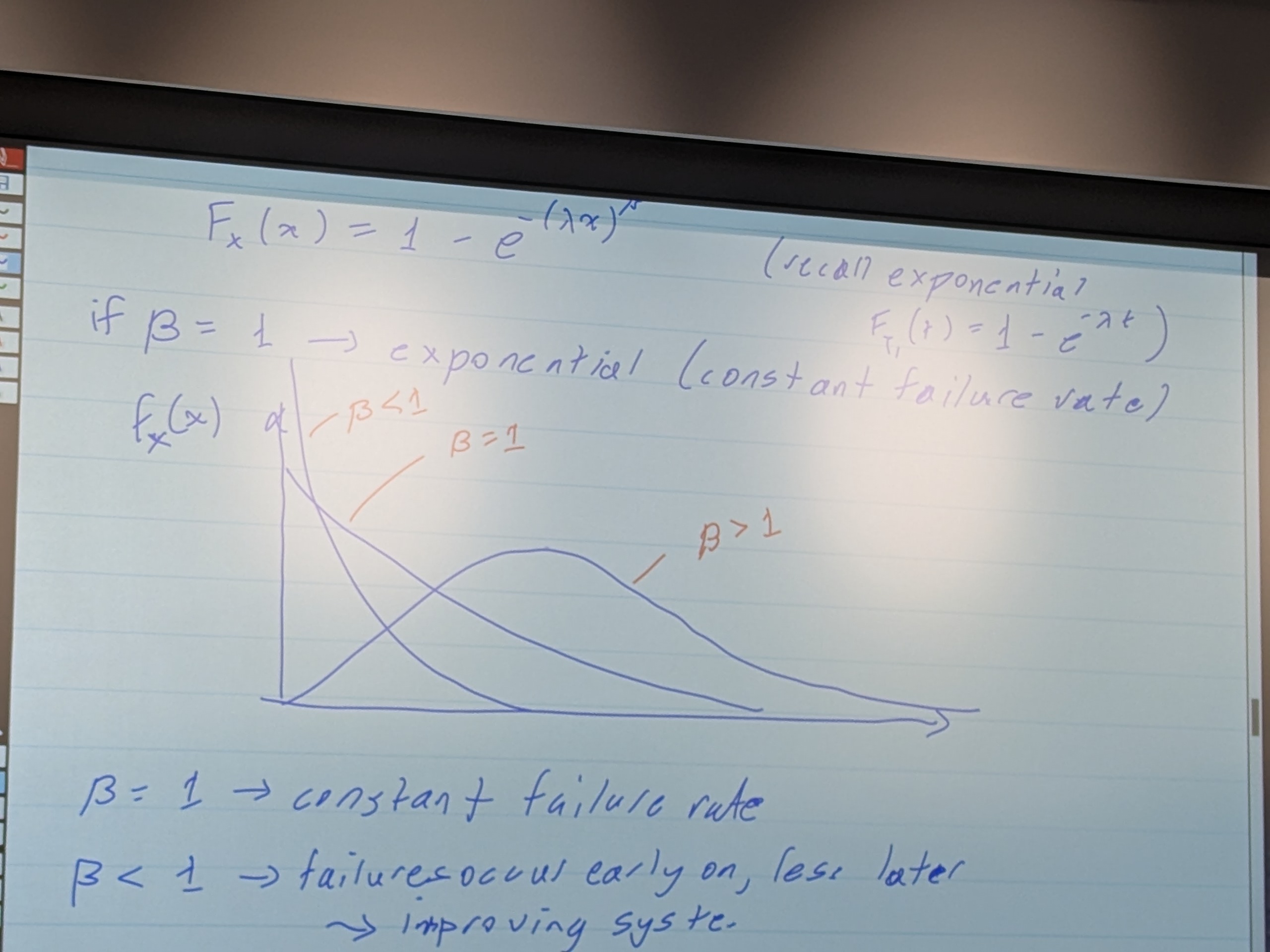
Weibull Distribution

There is a proof to say

Weibull Distribution

If B = 1 for big F(x), you’ve got an exponential, and a constant failure rate If B < 1 for big F(X), you tend to get more failures early on, and fewers failures later on - This is known as an improving system, eg, A.I, bacteria colony, red wine, glue, concrete (until it starts to fail, but initially, it takes time to set) If B > 1 for big F(X), you’ve got a degrading system. This is much more common.