Fields and the Laplacian

Laplacian (Δ)

The divergence of a conservative field is equal to the laplacian of the potential! It is marked as ΔF, or ∇²

Incompressible Fields

• The Curl of a conservative field will always be ZERO
• The Divergence of a incompressible field will always be ZERO

In 2D, an incompressible field is associated with stream functions (similar to potential functions)

• Incompressible fields have different markings!

$$\vec{v}=(\frac{d\psi }{dy},\frac{-d\psi }{dx})$$

compared to

$$\vec{v}=(v_x,v_y)$$

• Stream functions do NOT exist in 3D, only 2D

Conservative and Incompressible Fields

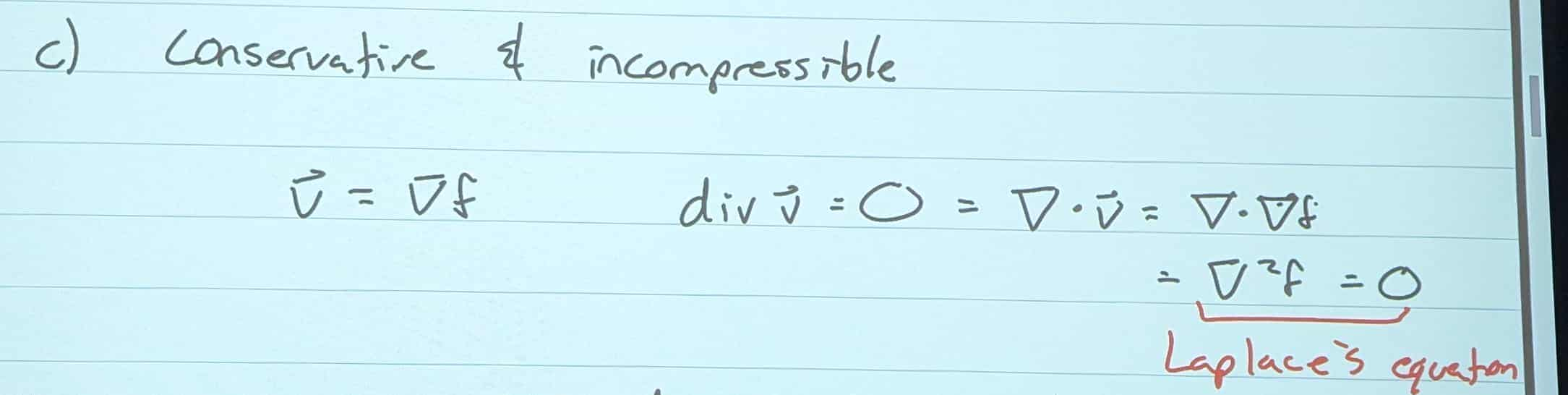
If conservative and Incompressible, the field will satisfy Laplace’s Equation

Fields and Curves

Recall that r(t)..

$$r(t)=(x,(t),y(t),z(t))$$

Over a range of t, we will generate a curve.

• We have seen this before!

Recall that the unit tangent vector T =

$$\hat{T}=\frac{\frac{dr}{dt}}{||\frac{dr}{dt}||}=\frac{\vec{v}}{||\vec{v}||}$$

• Recall our smooth curves!

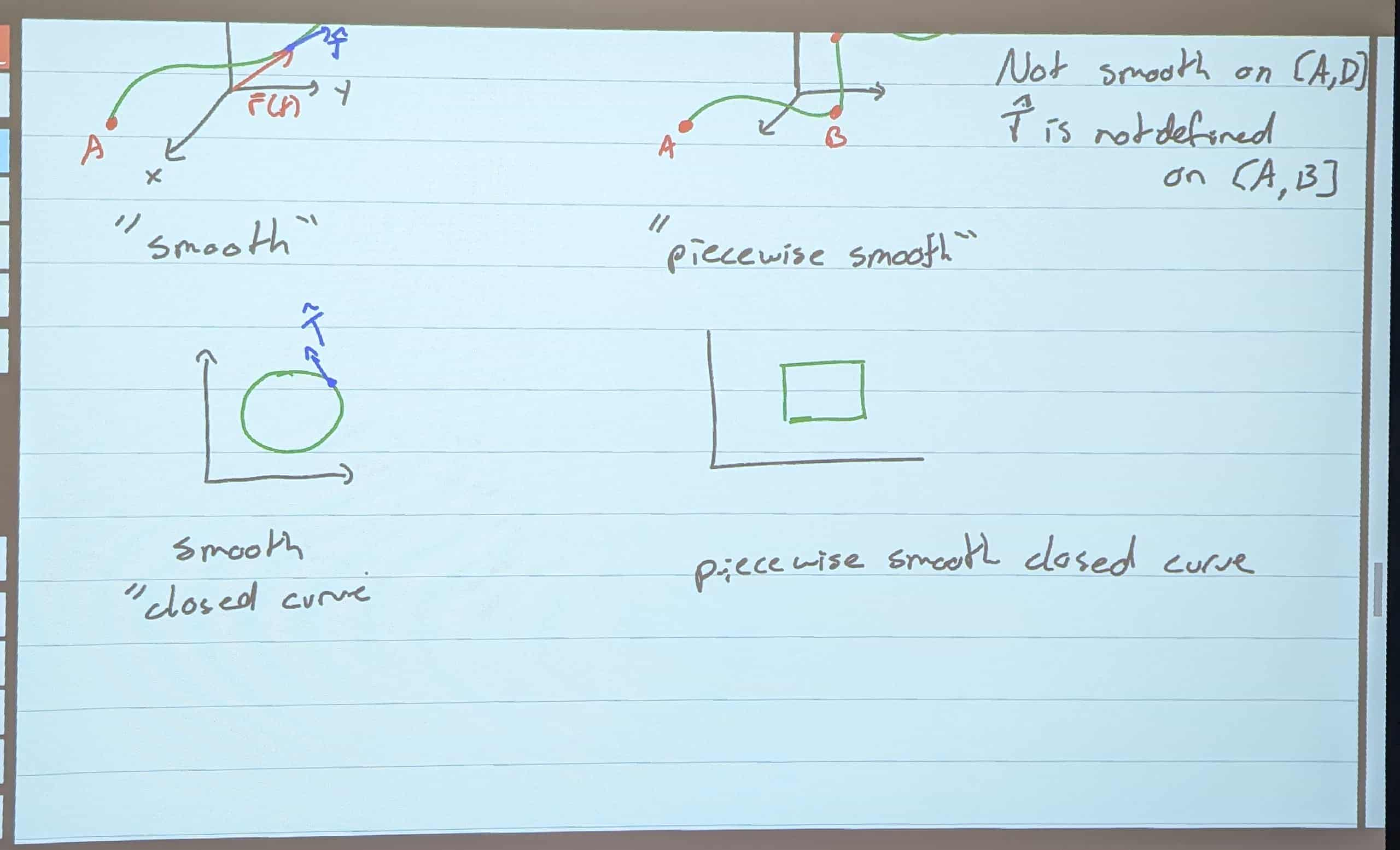
Convention

• We travel counter clockwise around the curve.

We can use these curves for our fields!

Scalar Fields f(x,y) or f(x,y,z) Curve r(t) = (x(t),y(t),z(t))

What is the scalar function along the curve?

Vector fields f(x,y) or f(x,y,z) Curve r(t) = (x(t),y(t),z(t))

What is f on curve?

• Plug in x(t), y(t) and z(t) from curve into f → f(t)

• We can break f into two components!

  • The Tangential Component
  • The Normal Component

\vec{f} = \vec{f}_\hat{T} + \vec{f}_\hat{N}

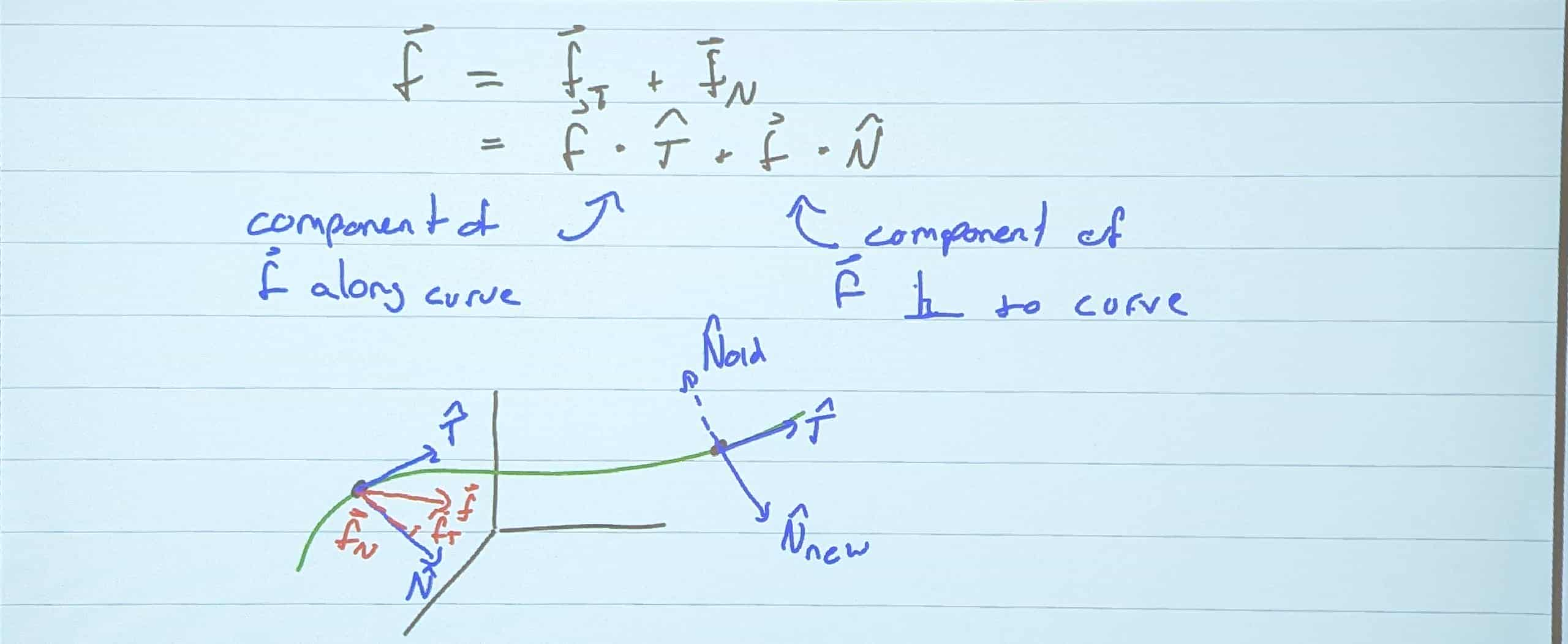
• One thing to note about N, is that it is not the same as it used to be!
• N now will face the other direction than it did previously
• Before, N used to face inwards during the curve.
• Now, it faces outwards.

Now,

$$\hat{N}=\hat{T}\times \hat{K}$$

N is the normal T is the tangent K is the Khat from (i, j, k)