Calculus of Scalar and Vector Fields (Vector Calculus)

Scalar Fields

• Scalar Functions = f(x), f(x,y), f(x,y,z)
• Think of x,y,z as space (3D)
• Temperature T(x,y,z), is a scalar field
• The gradient of a scalar field, is a vector field

---

Vector Fields

Vector = magnitude and direction

• Velocity, Acceleration, Force

• When vectors vary in space, you have a vector field.

$$\vec{v}(x,y,z=v_x,v_y,v_z)$$ $$v_z(x,y,z)$$

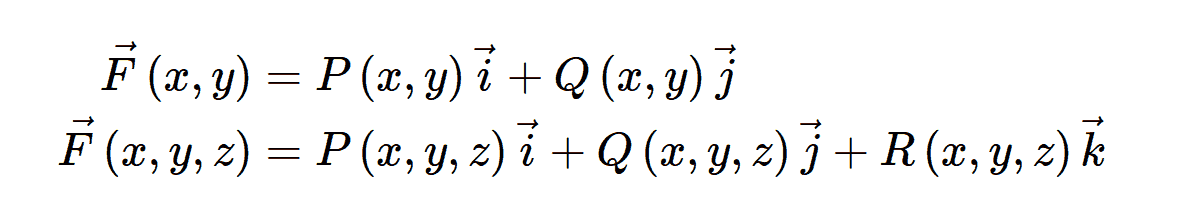
• Each component of a vector field can vary in space, and contains a scalar field.

Important Properties of Vector Fields

• Every field has the following properties that can be observed/studied/

• These properties can tell us how a field varies in space

• Gradience

• Divergence

• Curl

• Divergence is result of dot product, and measures 3 of the three derivatives available

  • Divergence measures the “Flow” of a point. If there’s stuff going in, or stuff going out of a point

• Curl is the result of cross product, and measures the other 6 of the derivatives available

  • Curl measures the “Rotation or swirl” around a point
  • If in 2D for curl, you must only keep the last term.

Special Cases

a) Conservative When v =∇f (f is the potential function for v)

Some examples of where this can occur:

• Electrical Force Electrical Potential

• Magnetic Force Magnetic Potential

• Gravitational Force Gravatational Potential

This case occurs when the curl = 0