Gram-Schmidt, QR Decomposition, Orthogonal Sets and Subspaces

Gram-Schmidt (Or G.S. for Short…)

Before we begin with G.S. I love this video explaining what is going on while doing G.S. Specifically the 2D part

• Dan starts with 2 vectors

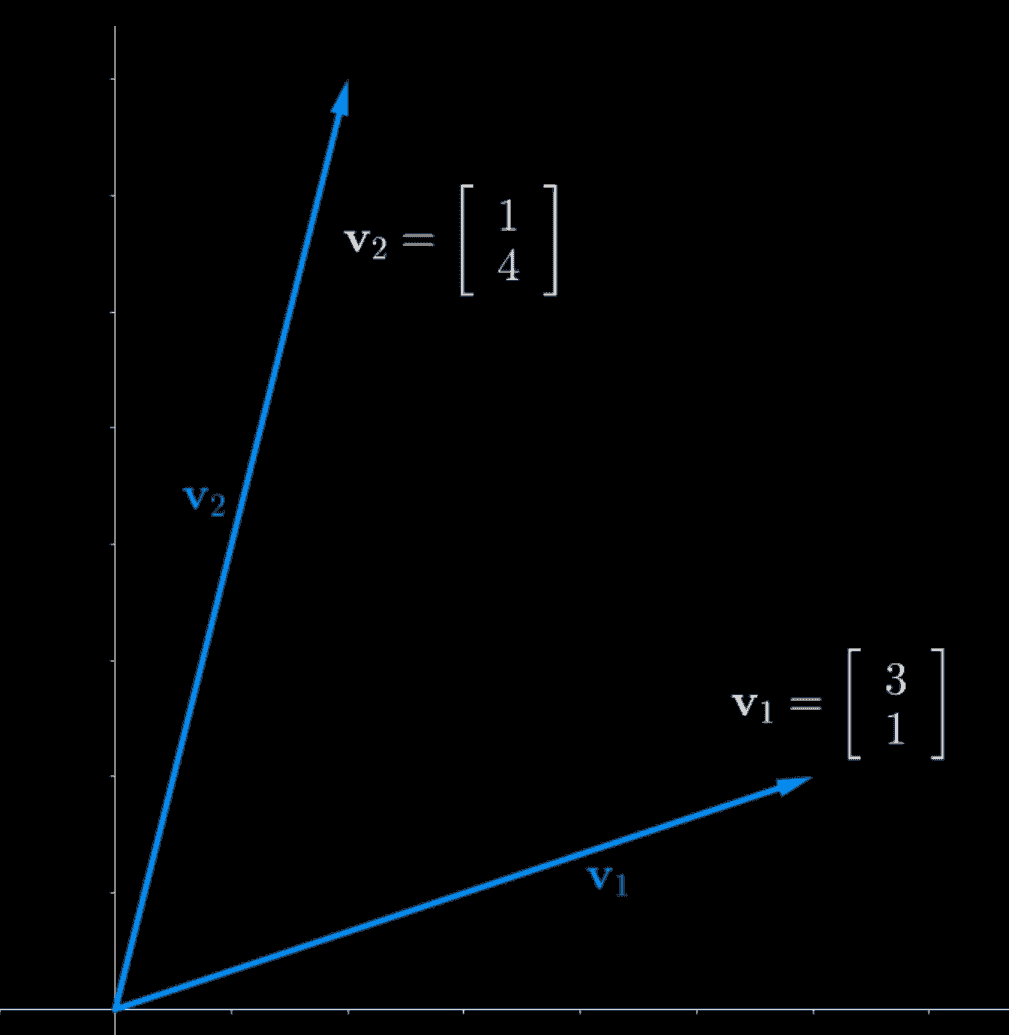
• He wants to find the orthonormal to vector V₁, using his vector V₂
• He begins by converting V₁ into a unit vector, to satisfy the normal part. This is actually known as normalizing a vector.
• He then projects V₂ on to the span of V₁. Dan now has his parallel component

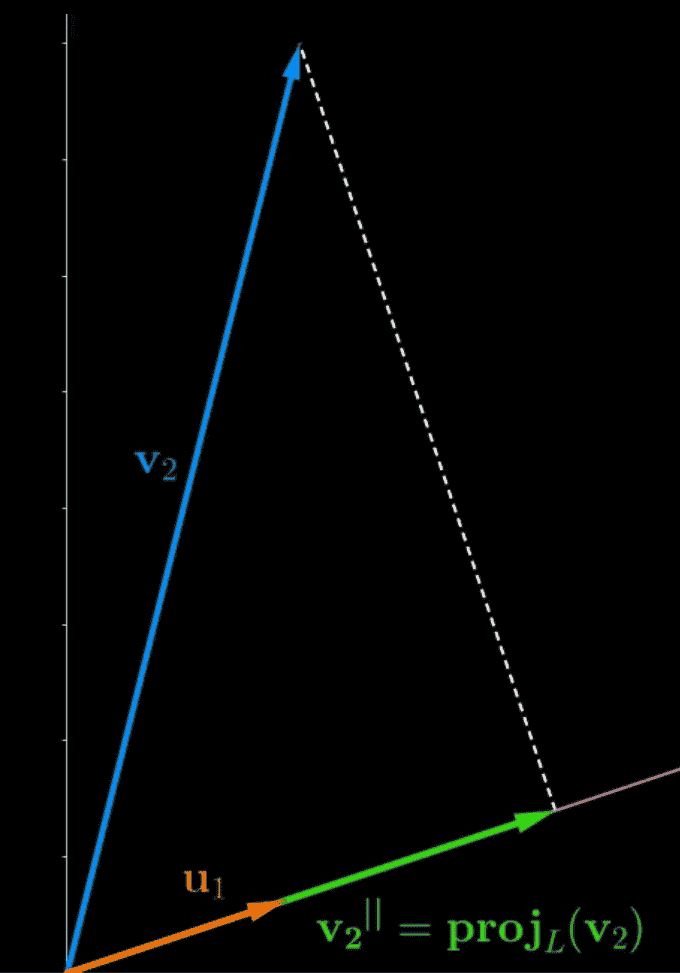
• Next, he subtracts his parallel projection from his V₂ vector, to find the orthogonal part

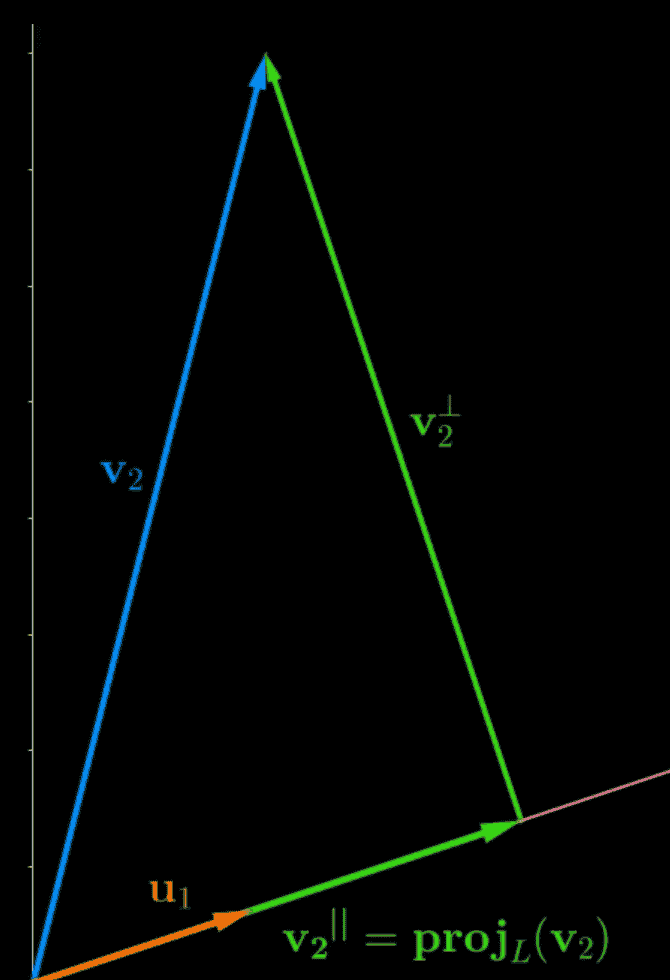
• From here, Dan normalizes his V₂ perpendicular vector (he also puts it on the Y axis now for clarity)

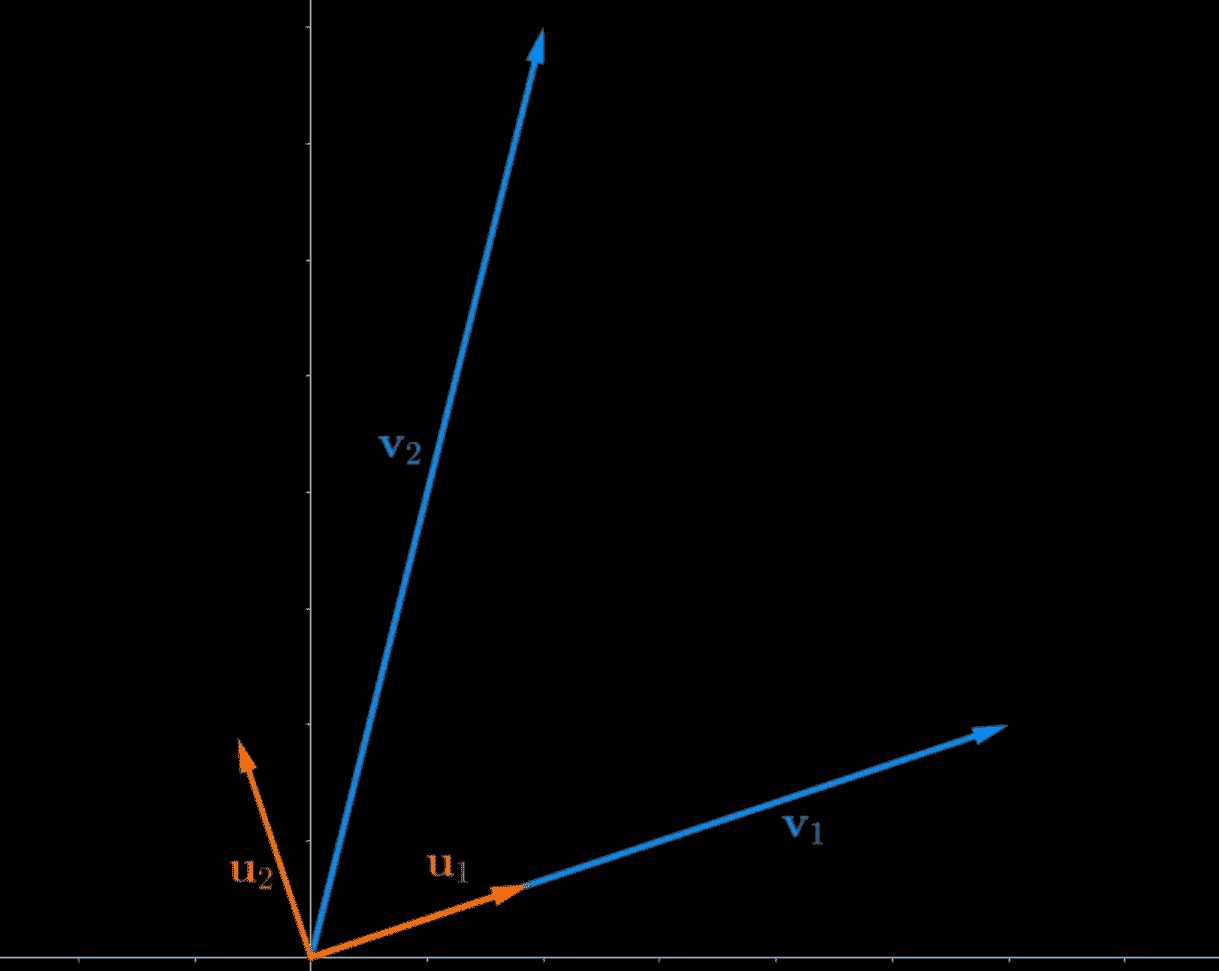
And just like that, it’s done. That is visually what is happening during the Gram-Schmidt Process.

—

Now, for the math/formula.

• Start with a series of basis vectors, defining a vector space.

$$\overrightarrow{v_1},\overrightarrow{v_2}...\overrightarrow{v_n}$$

• Now, for a solving pattern.

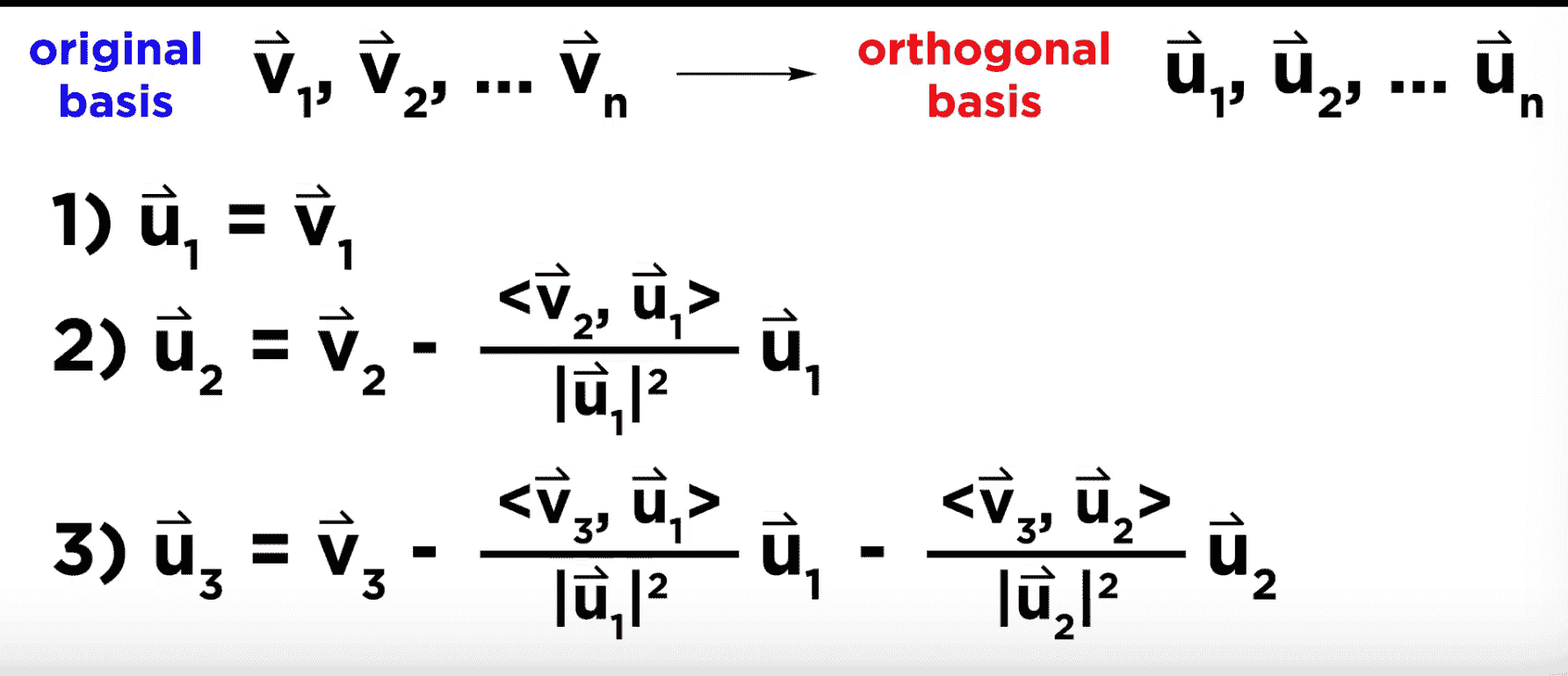
1. The first orthogonal basis is equal to the first basis vector. Makes sense.

2. The second orthogonal basis is equal to the second vector, MINUS the parts that are not orthogonal to the first basis! (shown earlier, what dan was doing!!) - An important thing to note here, is notice that the term being shaved off is just dot product!

3. Rinse and repeat. It’s the same thing over and over again, just adding another term of non-orthogonal parts to shave off!

Here is an example.

It is good to know, that when it’s all said and done, the thing that you are solving for with G.S, the Orthogonal Basis, is just this:

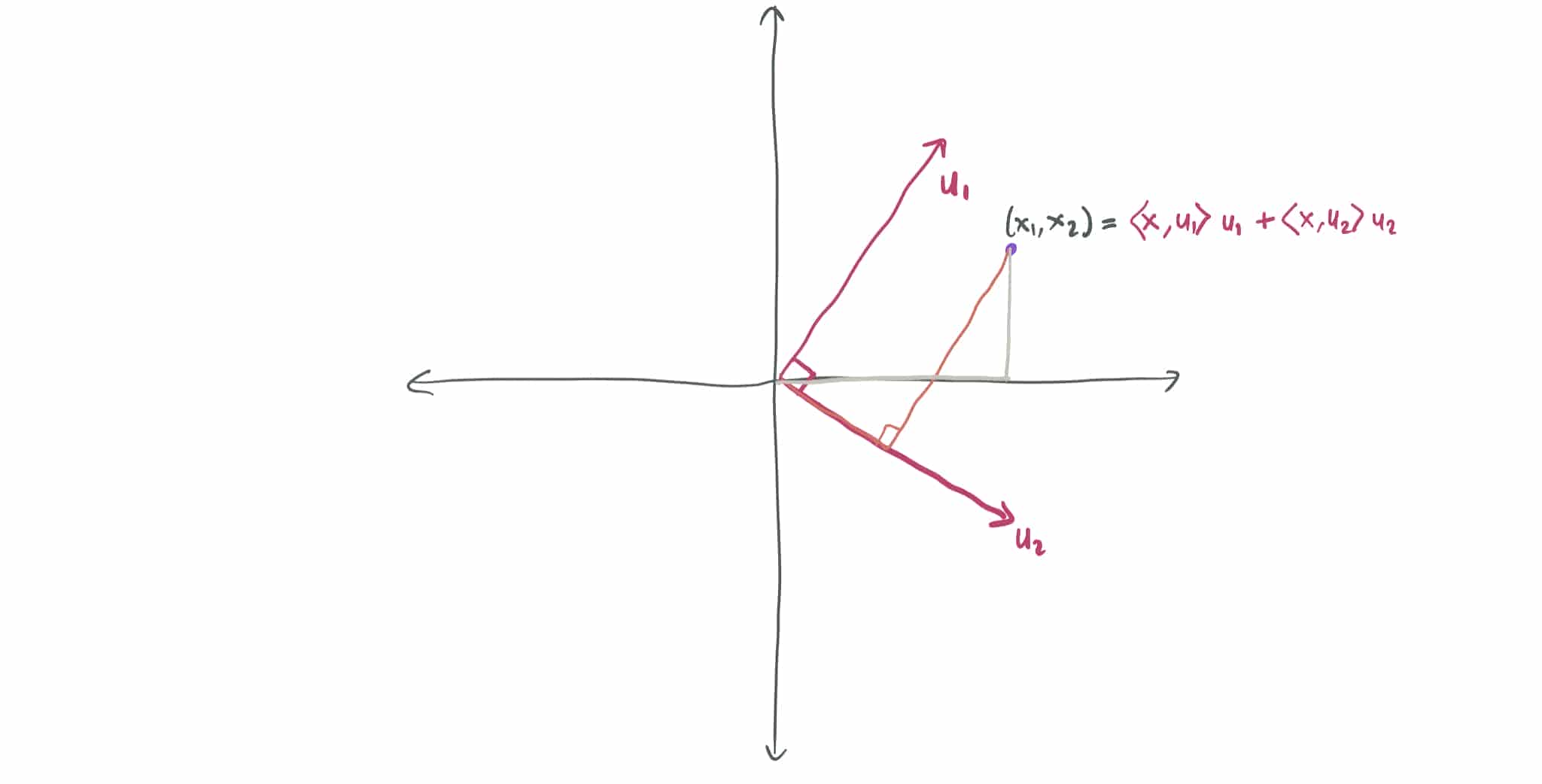Orthonormal Basis! ⮵

Just a fun way to transform two basis vectors into orthogonal vectors. Cool!