Distribution of a Sample Variance

Distribution of Sample Varience

$$S^2=\frac{1}{n-1}\sum _{i=1}^n(X_i-\bar{X}{)}^2$$

It turns out that the quantity

$${\chi }^2=\frac{1}{{\sigma }_x^2}\sum _{i=1}^n(X_i-\bar{X}{)}^2$$

is Chi-squared distributed with V = N-1 degrees of freedom

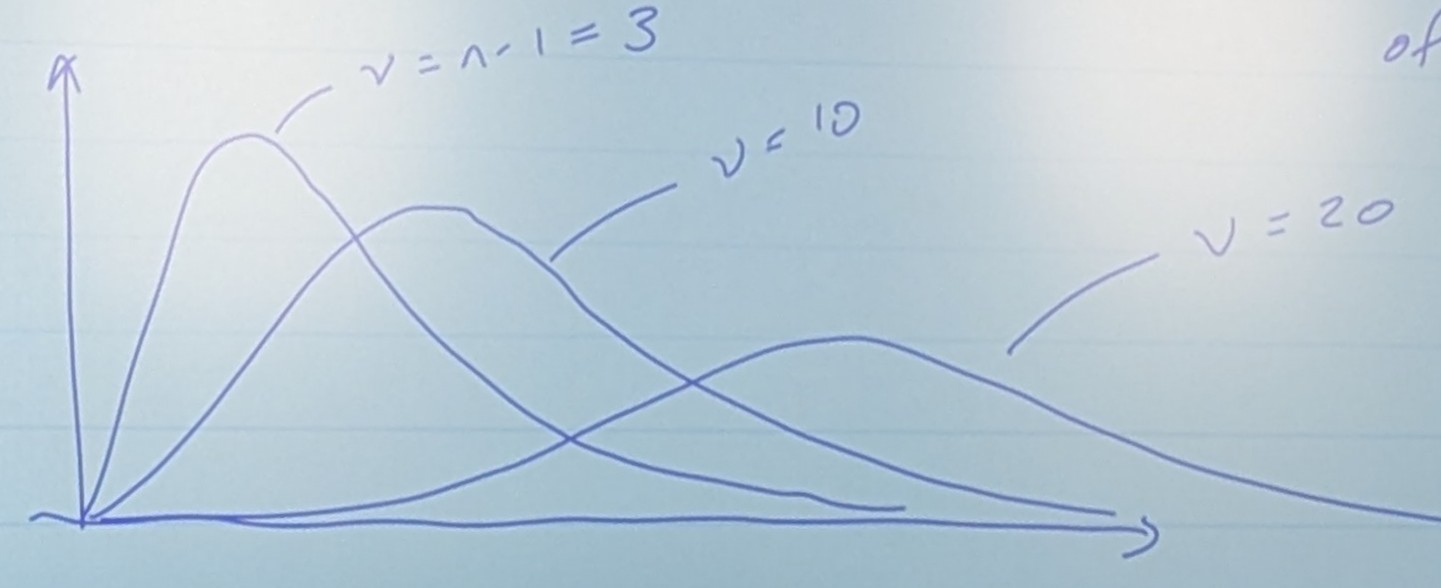
So consider

$$S^2=\frac{1}{n-1}\sum _{i=1}^n(X_i-\bar{X}{)}^2$$ $${\chi }^2=\frac{1}{{\sigma }_x^2}\sum _{i=1}^n(X_i-\bar{X}{)}^2=\frac{S^2(n-1)}{{\sigma }_x^2}$$

Where sigma follows a chi squared distribution with $\nu =n-1$ degrees of freedom.

So, we can now compute things like this

$$P(S_x^2>2{\sigma }_x^2)=\frac{S^2(n-1)}{{\sigma }_x^2}>2(n-1)$$

Chapter 6 Parameter Estimation (Confidence Intervals)

Point Estimates:

$$\bar{x}=\frac{1}{n}\sum x_i$$ $$S^2=\frac{1}{n-1}\sum _{i=1}^n(X_1{)}^2$$

Confidence Intervals

We want to come up with two numbers, L and U, such that $P(L\le {\mu }_x\le u)=1-\alpha$, where $1-\alpha$ is the confidence, and $\alpha$ is the significance.

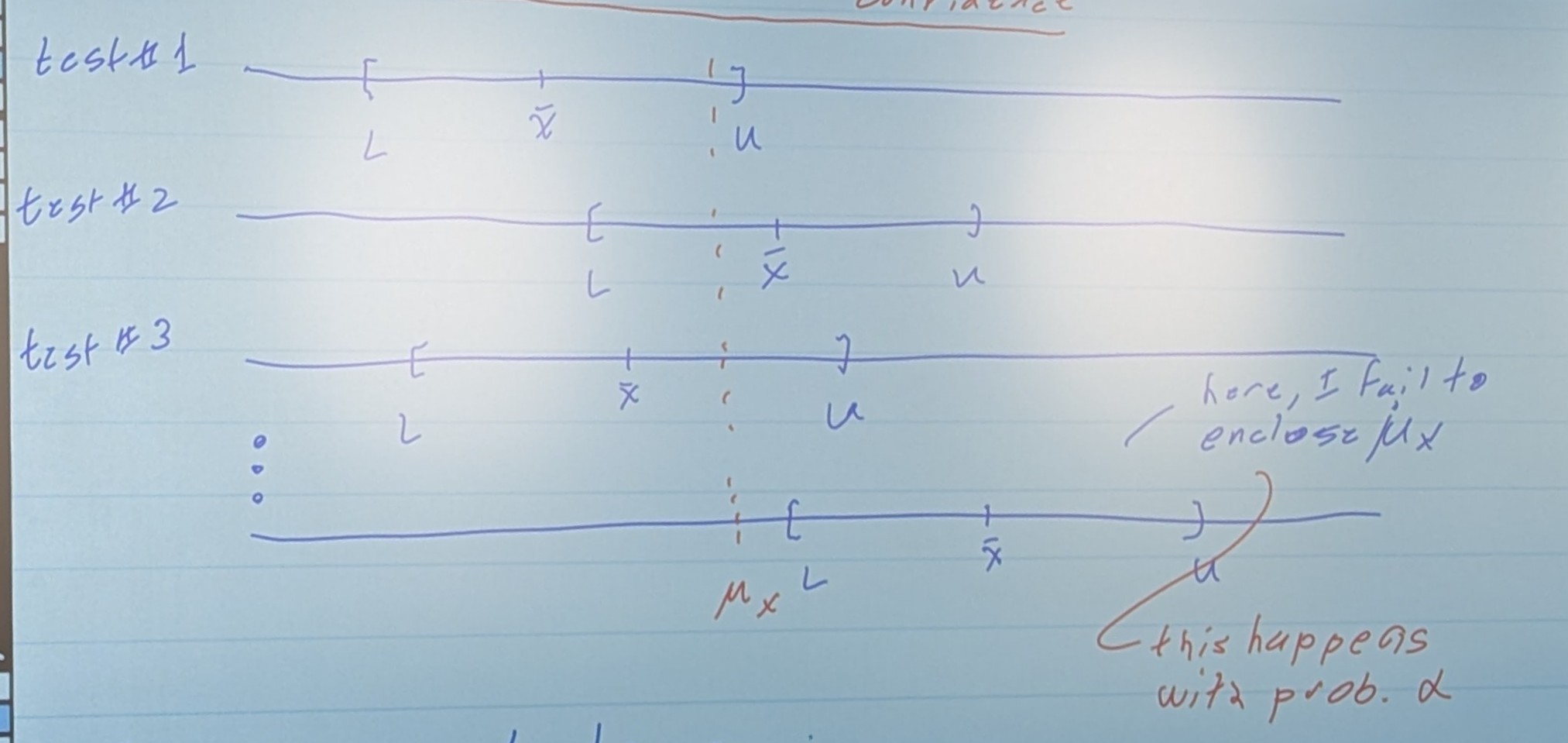
So choose $\alpha$ to be small, (but not too small)

• If $\alpha$ = 0, I’m 100% confident that {L,U} enclose the true mean, ${\mu }_x$
  • We would need $[L,U]$ = $[-\infty ,+\infty$]
  • Usually, $\alpha =0.05$ to $0.10$ is selected

How do we find L and U?

Consider

$$P(-Z_{\frac{\alpha }{2}}<\frac{\bar{X}-{\mu }_x}{{\sigma }_x/\sqrt{n}})$$

There is a proof to say that

$$[L,U{]}_{1-\sigma }=\bar{X}\pm Z_{\frac{\alpha }{2}}\frac{{\sigma }_x}{\sqrt{n}}$$

If we are finding a confidence interval on ${\mu }_x$ then,

$$(L,U)=(\bar{X})\pm (Z_{\frac{\alpha }{2}}\underline{\text{or}}{t}_{\frac{\alpha }{2}},v)({\sigma }_{\bar{X}})$$

If we are finding a confidence interval on ${\mu }_{x}1,-{\mu }_{x}2$ where ${\sigma }_{x}1$ and ${\sigma }_{x}2$ are known, then

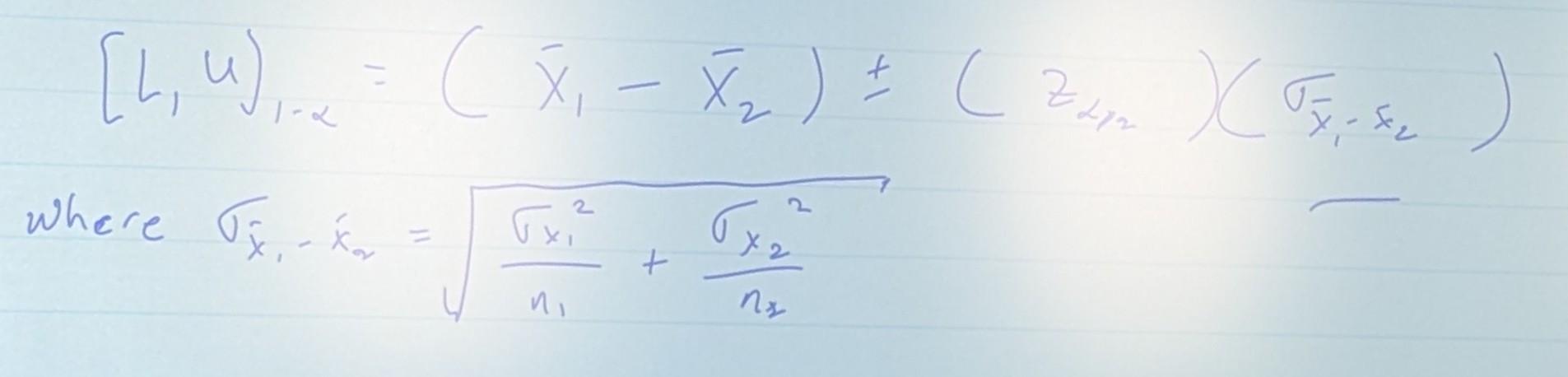
We sometimes want to just know a one-sided confidence bound, i,e L or U individually:

---

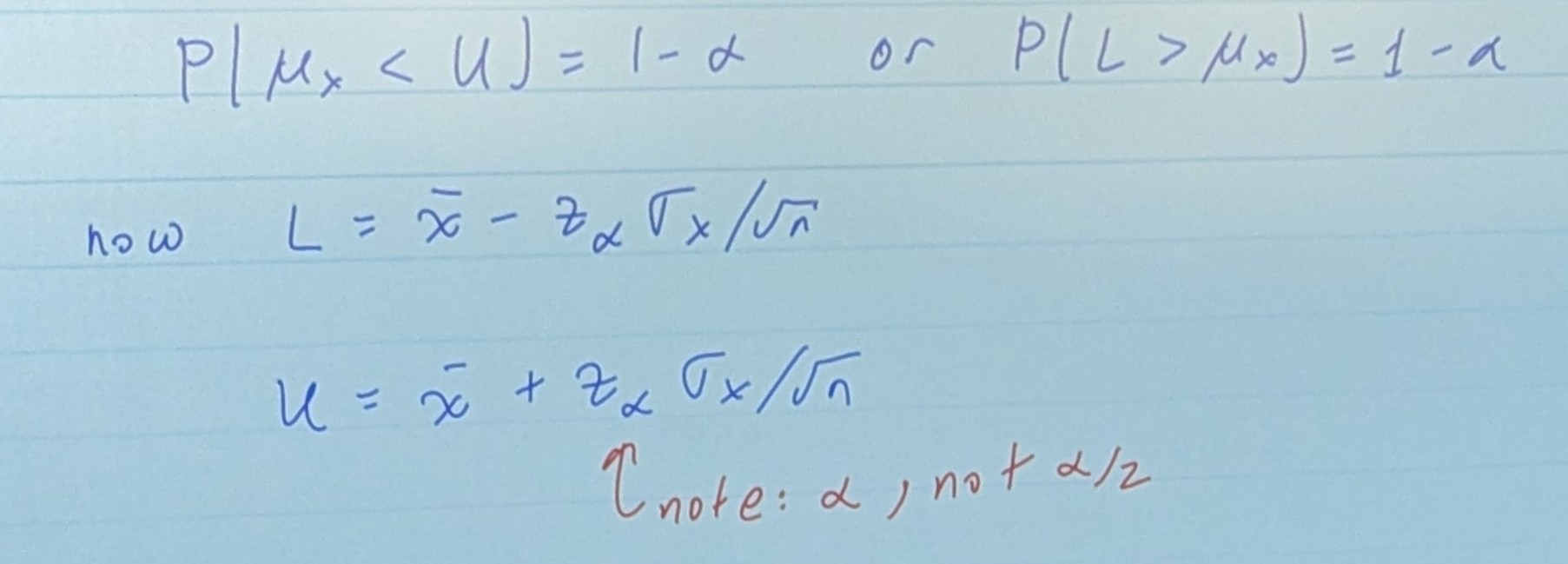
Example 1

Example 2

We are told $\bar{X}=960$, $n=25$, ${\sigma }_x^2=225({\sigma }_x=15)$ (sigma is known, use Z)

$$(L,U)=(\bar{X})\pm (Z_{\frac{\alpha }{2}})({\sigma }_{\bar{X}})$$ $$(L,U)=(\bar{X})\pm Z_{\frac{\alpha }{2}}(\frac{{\sigma }_{\bar{X}}}{\sqrt{u}})$$ $$(L,U)=(960)\pm Z_{0.025}(\frac{15}{\sqrt{25}})$$ $$(L,U)=(960)\pm (1.960)(\frac{15}{\sqrt{25}})$$ $$=[954.1,965.9]$$

We are 95% confident that the true ${\mu }_x$ is in this interval.

---