Common Distributions and Bernoulli Trials

Chapter 4: Common Distributions

Discrete Distributions

Bernoulli Trials:

• A sequence of trials each having
  1. Two possible outcomes
  2. Constant probability of “success”
  3. Trials are independent

In the theory of probability and statistics, a Bernoulli trial is a random experiment with exactly two possible outcomes, “success” and “failure”, in which the probability of success is the same every time the experiment is conducted.

An example of this would be a coin toss, the probability doesn’t change each flip!

Let’s define an X_i here:

X_i = 1, if the i^th trial is a “success” X_i = 0, if the i^th trial is a “failure”

and let

P(X_i = 1) = p P(X_i = 0) = 1 - p = q

🡹 This here, is a Probability Mass Function (PMF)

Where E(X_i²) = (1)²p = p(1 - p) = pq

This leads to distributions:

Binomial Distributions

$$\text{Let}{N}_n=\sum _{i=1}^n{X}_i=(0+1+1+0+1+0+\mathrm{0..})$$

i.e equalling

= number of “successes” in n trials.

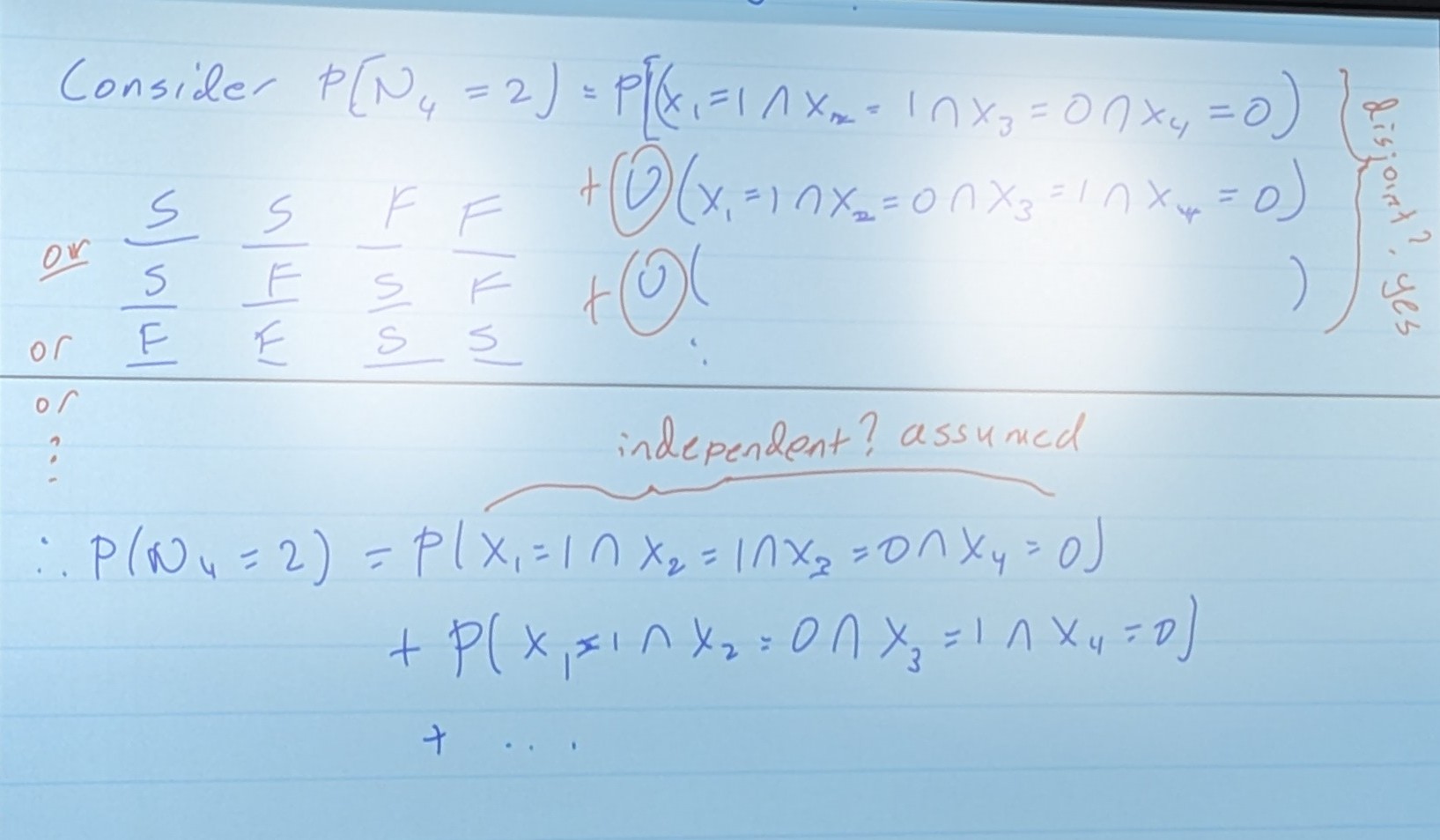
= p²q² + p²q² + …

= (Four choose Two “4 over 2”) * p²+q²

General Formula for distributions

$$P(N_n=k)=\left(\genfrac{}{}{0ex}{}{n}{k}\right)p^k{q}^{n-k},\text{for}k=1,2,\mathrm{3...}n)$$

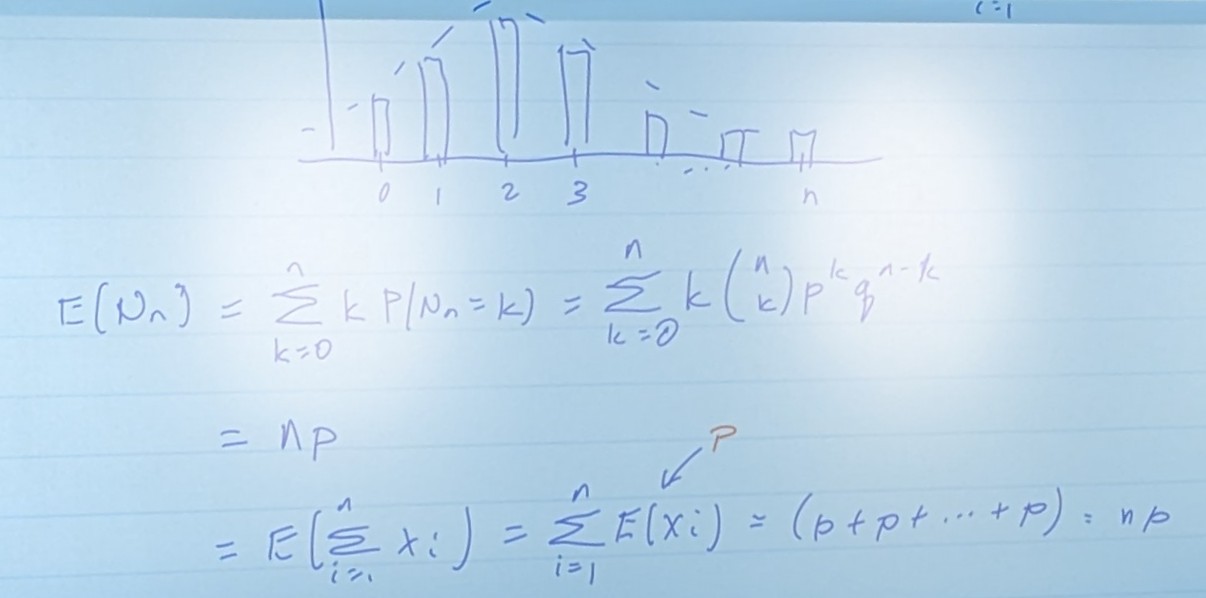
Varience for Bernoulli Trials

$$Var[\sum _{i=1}^n{X}_i]=\text{Sum}\text{of}\text{variances}\text{since}\text{assumed}\text{independent.}$$ $$Var[\sum _{i=1}^n{X}_i]=(pq+pq+pq+...+pq)$$

since X_i = pq

$$=npq$$

Example 1

Example 2

This is a sequence of Bernoulli Trials. Because of this, we can assume independence. Without that piece, this is not solvable.

N¹⁰ = Number of failures in N trials

We want to find

$$P[N_{10}\ge 2|N_{10}\ge 1]$$

Recall That...

$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

So…

$$P[N_{10}\ge 2|N_{10}\ge 1]=\frac{P[N_{10}\ge 2\cap N_{10}\ge 1]}{P(N_{10}\ge 1)}$$ $$\frac{P[N_{10}\ge 2]}{P(N_{10}\ge 1)}$$

Worked out that is…

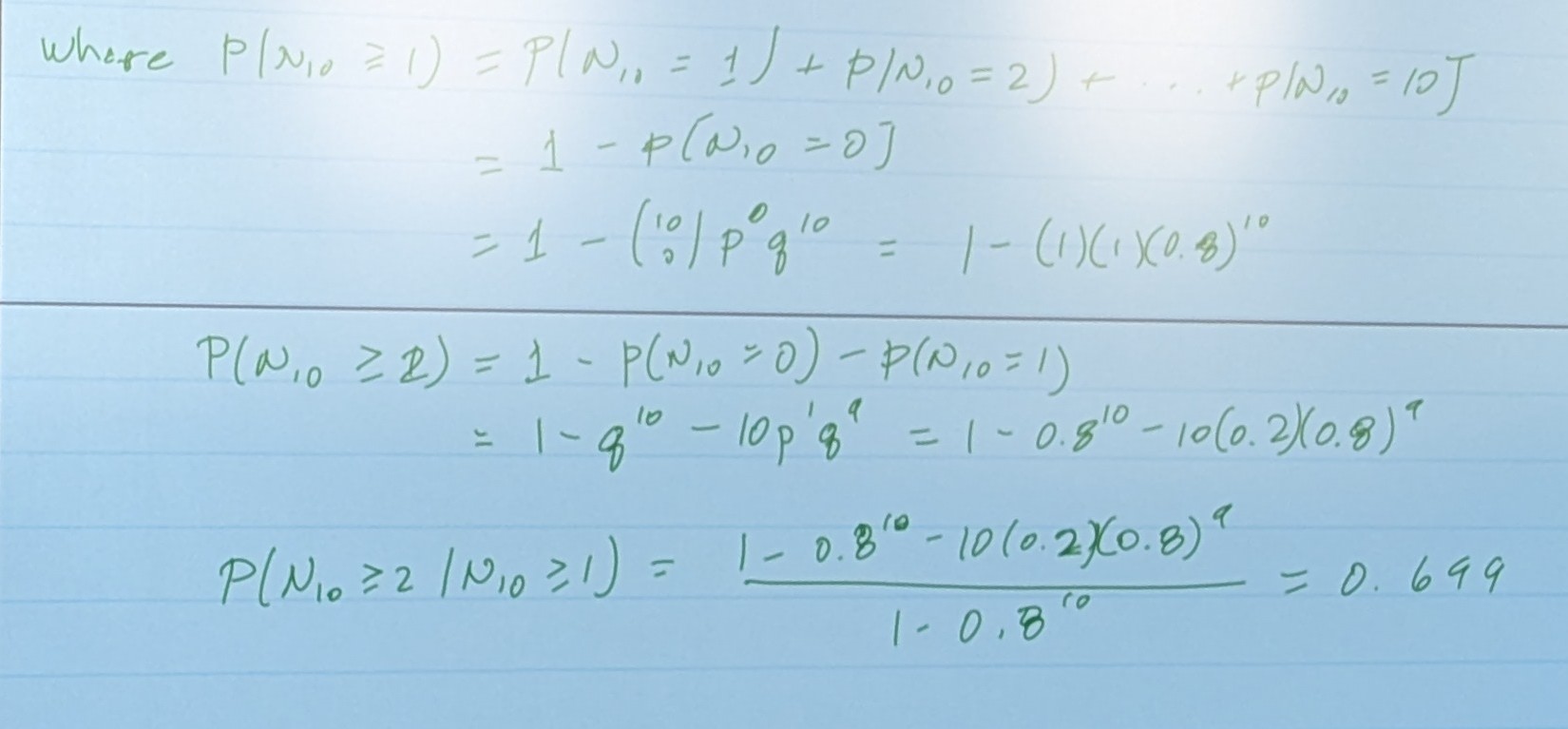
Geometric Distribution

Let T₁ = Number of trials until the first (or next) “success”

Distribution?

P(T₁ = K) = ?, K = 1,2,… , ∞

$$P(T_1=k)=p{q}^{k-1},k=1,2,..,\infty$$

---

Summary of Statistics Distributions